　身近な振動の代表が“振り子”である。振り子を手に持ち、錘（おもり）を離すと錘は振動する。この状況（振り子の自由振動）を、式で表現したのが図5である。単位時間に何回振り子が往復するかを「固有振動数」と呼ぶ（図8で再度説明する）。すなわち、振り子の固有振動数は錘の質量にはよらず、振り子の長さと重力加速度に依存する。また、正確には、振り子の振動振幅が大きい場合には、いわゆる「非線形振動」となり、振り子の場合、振動数は微小振幅のときに比べて低減する（ゆっくり振れる）。

　振り子を利用したものに“振り子時計”がある。この場合、振り子の非線形性は時計の精度に影響する。そこで、「サイクロイド曲線」に沿って振り子を振らせることにより、有限の振幅でも等時性（周期一定）を実現したのが「サイクロイド振り子」である。サイクロイド振り子は、クリスティアーン・ホイヘンスによって1657年に考案された（参考文献［1］［2］）。

図5　振り子の振動：自由振動［クリックで拡大］

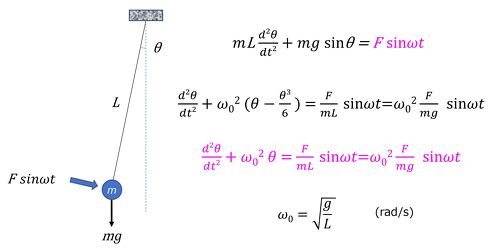
　一方、振り子の錘を外部から加振した場合が、振り子の強制振動で、図6に示す形式で表現される。この解法は、後ほど図10で説明する。

図6　振り子の振動：強制振動［クリックで拡大］

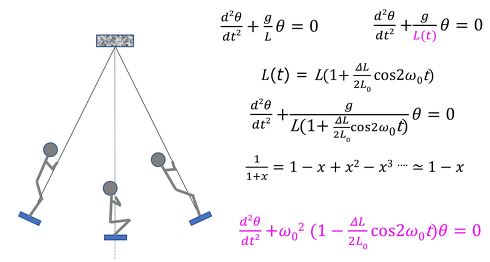
　振り子の応用例として、ブランコがある。ブランコでは外部から入力がないのに振動を発生させることができる。この原理を図7で説明する。ブランコは人が乗って遊ぶ遊具である。その状況を観測すると、人は立ったり座ったりしていることが分かる。振れの両端では立った姿勢で、最下点では座った姿勢になっている。このことは、振り子の長さが時間とともに変化していることを意味する。すなわち、振り子の長さLが定数ではなく、振り子が1周期する間に2周期の長さの変化が発生する。この様子を図中の式で表現している。

　最終的には「係数励振振動」という自励振動の一種で表現できる。これも非線形振動の一種で解析的に解くことはできず、近似解法または時刻歴応答解析で解くことになる、ここで重要な事実は“人の漕ぐ周期が振り子の周期の2分の1のときに自励振動（振動振幅が時間とともに発散する）が発生する”ということだ。これは“振り子の固有振動数の2倍の振動数で漕ぐと自励振動が発生する”と表すこともできる。ブランコはこの原理で（無意識のうちに）振れているということである。