解析結果を左右する「構造」と同じくらい重要な“その他の要因”とは：構造解析、はじめの一歩（8）（1/3 ページ）
「構造解析」を“設計をより良いものとするための道具”として捉え、実践活用に向けた第一歩を踏み出そう。第8回は、解析結果を大きく左右する「構造以外の要因」について着目し、その重要性をステップ・バイ・ステップで分かりやすく解説する。
はじめに
※注意※
- ヤング率、ポアソン比など、基本的な材料力学の知識があることを前提としています。材料力学の知識を持たずして解析を行うことは、免許を持たずしてクルマの運転をするのと同じことです。「危険」であることを心得ておいてください
- ソフトウェアのインストールや使用については、自己責任ということでお願いします
- 今回の記事は、連載第5回の「線形静解析」で説明した部分が大幅に省略されています。ぜひそちら（連載第5回）の記事に目を通してからご覧ください
ここまで、座学とCAEの必要性、設計者CAEのベースとなる3次元CADモデル、そして、設計者CAEの登竜門である「線形静解析」と「固有振動数解析」について解説してきました。
これまで話の中心は構造物であるモノでしたが、今回は「構造」以外のことについて解説したいと思います。構造以外の要因も解析結果を大きく左右します。より精度の高い解析結果を得るためにも、構造以外の要因は構造そのものと同じくらい重要です。
応力の算出に必要な3要因
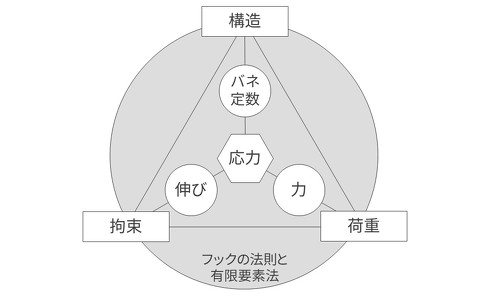
線形静解析の場合、「応力」は次の3つの要因で決定します（図1）。
「構造がない」ということは、そもそも「解析する対象物がない」ということですから応力は発生しようがありません。
「拘束」とは固定のことです。拘束がないと、モノは「荷重」をかけた方向にすっ飛んでいきます。ただし全てのモノが固定されているわけではありません。例えば、飛行中の飛行機はどこも固定されていません。
荷重がないと、モノにチカラが作用しません。よって応力も発生しません。ただし、実際にはモノには自重があるので、わずかながら自重によるチカラが作用しています。一般的に自重により発生する応力はごくわずかですが、大きな加速度がかかるモノですと自重は無視できません。
図1に示す3つの要因（構造、拘束、荷重）の中で一番分かりやすく、完成度が高いのが構造です。なぜなら、3D CADによって詳細に形状が作り込まれるからです。細いスリットから小さな穴まで、図面には必要な要素ではありますが、CAEには必要のない、むしろ弱点となるような詳細な形状まで作り込まれています。
次に分かりやすいのが拘束です。モノがどのように固定されているのかは大体の場合、観察することができます。ボルト、溶接、接着剤、リベットなど、固定方法は見れば分かります。
これらに対して、一番分かりづらいのが荷重です。機械内部の部品であれば、荷重のかかり方は特定できますが、ユーザーが関わる部分では、設計者の想定外の荷重がかけられる場合があります。
モノの体積内部を固定したり、荷重をかけたりすることはできないので、通常、拘束や荷重はモノの表面に関係があります。よって、拘束条件や荷重条件をまとめて「境界条件」といいます。
筆者は、これまで設計者の行ったたくさんの解析事例を見てきましたが、構造、拘束、荷重の粒度がかなり偏っている場合が多くあります。この粒度が合わないと、せっかくの精度の高い形状モデルも無意味になってしまいます。
有限要素法とフックの法則
有限要素法の計算
構造、拘束、荷重の3要因の粒度を合わせることがなぜ重要なのかをしっかりと理解していただくために、少々遠回りになると思いますが、「有限要素法」の計算の仕組みと有効数字について説明します。
有限要素法を難しい式で表現すればキリがないので、ここではできるだけカンタンに、有限要素法で行われている計算の内容を解説します。
有限要素法は、非常に大ざっぱにいえば、「フックの法則」を解いているにすぎません。フックの法則は中学校の理科の授業で学びます。
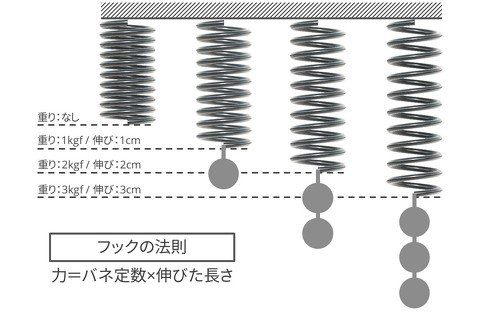
バネに力をかけると伸びます。“その伸びた長さはかけた力に比例する”というのがフックの法則です。その比例定数が「バネ定数」です。式で表すと以下のようになります（図2）。
以下のWebサイトでは、バネを直列につなげた場合や、並列につなげた場合を分かりやすく説明しているので、ぜひ参考にしてみてください。この複数のバネがそれぞれの有限要素だと思って読むと、フックの法則と有限要素法の関係がよく分かると思います。
有限要素1つを1個のバネだと捉えれば、有限要素の集合体の構造物はバネのカタマリであると考えることができます。構造全体のバネ定数のことを「剛性」といいます。
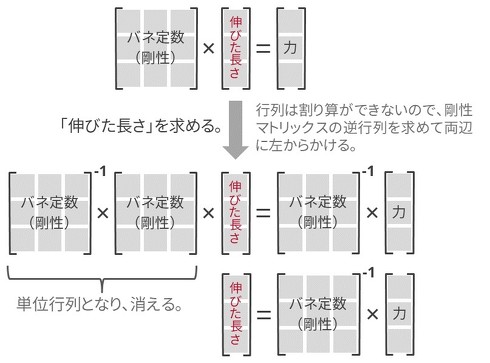
有限要素法では、フックの法則のバネ定数の部分は「行列（マトリックス）」で表現されます。これをフックの法則に代入して「伸びた長さ」、つまり構造物の「変形量」が算出されます。
伸びた長さを求めるためには、バネ定数の逆行列と力をかけ算する必要があることを覚えておいてください。
伸びた長さが“ゼロ”であることが“固定されている”ことになるため、拘束は伸びた長さに含まれます。
ちなみに、有限要素法による計算時間の95％は、剛性行列を組み立てることと、その逆行列を求めることに使われます。図3の式から分かるように、一度、剛性行列の逆行列を作れば、後は荷重を入れ替えるだけで、その荷重による変形量が計算されます。これが「荷重ケース」で、複数の荷重を合理的に計算処理するための考え方です。
Copyright © ITmedia, Inc. All Rights Reserved.
よく読まれている編集記者コラム
ITmediaはアイティメディア株式会社の登録商標です。