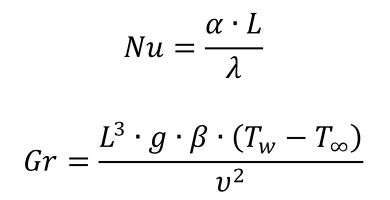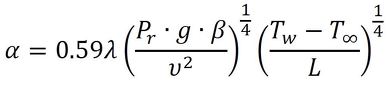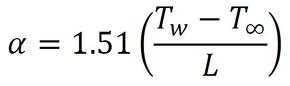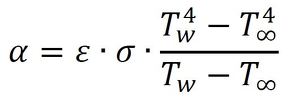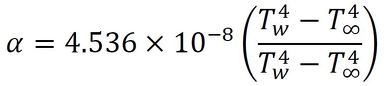　材料の熱伝導率であれば、材料固有の数値が明確に決まっています。ところが、熱伝達係数の場合は、曖昧なことが多いのです。実際、参考になる書物や資料を見ても、実に幅が広く、例えば、空気の熱伝達係数については、自然対流の場合、2～20W/m²、また強制対流の場合、20～250W/m²とかなりの幅があります。当然、この幅の一番高い数値を使ったときと、低い数値を使ったときとでは結果が異なってきます。

　実験などをしていれば、その結果を参考に“確からしいもの（熱伝達係数）”を決めることもできますが、アバウトと言えばアバウトです。より厳密に熱伝達を考えていく必要がある場合には、“熱流体解析と併せて考えなければならない”と言われたりもします。

　ということで、熱流体解析を行っていく上で、自然対流と強制対流の解析についても併せて考えていきたいと思います。なお、本稿はあくまでも「CFD（流体解析）ソフトを使ってやってみる」という観点での説明にとどまっているので、詳しい熱輸送のメカニズムについては、専門書や教科書などをご覧ください。

　また、今回から少しだけ理論と併せて解析を活用していきたいと考えています。そのため、普段から筆者が仕事でお世話になっている法政大学理工学部教授の御法川学先生にもご協力をいただいております。

自然対流による熱伝達

　自然対流による熱伝達のメカニズムは、熱せられた空気が膨張することで浮力が発生し、自然に上昇気流が発生することによるものです。

　例えば、一辺が100mmで、表面温度が120℃の立方体が、20℃の空気中にあるとします。この場合、自然対流の熱伝達率は、以下のような無次元化された式で表現できます。

　Nuはヌセルト数、Grはグラスホフ数、Prはプラントル数です。NuとGrは、さらに以下のように表現されます。

　Lは長さ、αが熱伝達率、λは流体の熱伝導率、gは重力加速度、βは体膨張係数、νは動粘性係数、T_wは平板表面温度、T_∞は流体温度を表しています。

　では、空気に対する自然対流熱伝達率の式を求めてみます。まず、前述の3つの式を使って、熱伝達率αの式に変形します。

　これに数値を代入します。温度が20℃の場合、流体の熱伝導率は0.256W/mK、Prは0.71、動粘性係数は0.154×10^-4m²/s、また体膨張係数は、絶対温度で表した流体温度の逆数になります。これらの数値を代入した結果は以下の通りです。

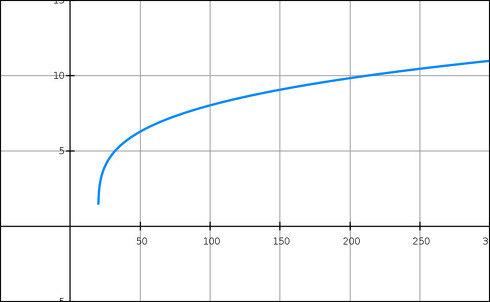
　これをグラフにプロットしてみると、

のようになります。ちなみに、ここまで説明してきた式は、あくまでも垂直平板に対するものです。そのため、今回のような立方体となると若干の違いがあると思います。とはいえ、この式を適用してもおおむね問題はないでしょう。理論的に他の形状、例えば、円柱などの熱伝導率を求めたい場合には、伝熱工学のテキストなどを参照してください。

　さて、もう1つ考えておきたいものがあります。それが輻射熱伝達です。輻射熱伝達は、以下のような式で求められます。

　εは輻射率、σはステファンボルツマン定数です。ここで輻射率を0.8と置いたとき、この式は、

となります。なお、輻射の計算を行う場合、計算に使用する温度はセ氏ではなく、絶対温度であることに注意してください。

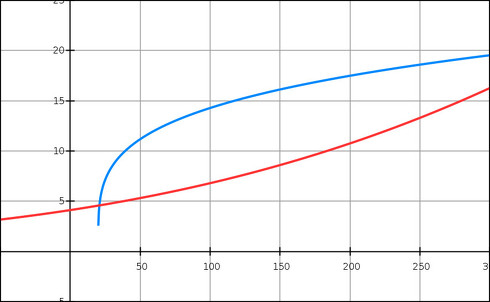
　今度はLの長さを10mmにして、対流の熱伝達係数と輻射の熱伝達係数を計算し、グラフにプロットしてみると、以下のようなグラフが得られました。

　上図の青色の線が対流熱伝達率、赤色の線が輻射熱伝達率を表しています。

　熱伝達係数に着目して、上図（Lが100mm）の係数と比較すると、大きくなっていることが分かります。つまり、Lもまた熱伝達率に影響を与えていることが分かります（式を見れば一目瞭然ではありますが）。また、輻射と比較すると、対流の場合、温度差が大きくなると上昇率は緩やかになりますが、輻射率の場合、上昇率はより急激に変化していきます。

手計算と流体解析ソフトの結果の比較

　　　　　　 1|2 次のページへ