解析結果に大きく影響する「乱流モデル」を考える：初心者のための流体解析入門（5）（2/3 ページ）

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

DNS：直接数値シミュレーション

　「DNS」は“直接数値シミュレーション”という言葉から連想されるかもしれませんが、乱流のモデル化ということは行わず、「ナビエ・ストークス方程式」をまさしく“直接”計算することになります。

　具体的には、流れの中にある全ての大きさの渦、つまり非常に小さな渦まで全て計算しなければならず、極めて小さなメッシュ、別の言い方をすると膨大な数のメッシュが必要になります。それ故、製品開発などで使用する手法としては非現実的であるといえます。

LES：ラージエディシミュレーション

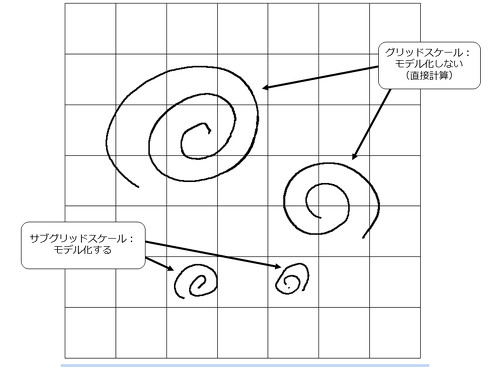
　これに対し、LESはある大きさの渦については直接計算を行い、小さな渦についてはモデル化するという、流体解析の初心者にとってある種“良いとこ取り”に聞こえる方法となります。実際、日常的に解析を行うシーンでは、RANSのいずれかのモデルを使用することがほとんどだと思いますが、昨今ではLESでの計算も計算環境の向上に伴い現実的になりつつあります。

LESにおけるメッシュサイズと渦の大きさの関係を示した概念図

　平均場のみにフォーカスした後述のRANSと違って、より解析精度は高くなるので、「可能であればLESで計算したい」というニーズも当然あるでしょう。ただし、計算時間はRANSと比べて、（ものにもよりますが）10倍から100倍はかかるため、計算負荷が非常に大きいといえます。

RANS：レイノルズ平均モデル

　そして、RANSです。端的に言えば、RANSは乱流の平均場を求めるもので「時間平均モデル」と呼ばれます。先のLESが3次元、非定常解析でなければならないのに対し、RANSは定常解析も可能で、基本的にLESほどの計算リソースは不要であるため、こちらの方がよく使用されます。商用ソフトでもRANSの「k-εモデル」や「k-ωモデル」がデフォルトになっているのではないでしょうか。

　k-εモデルは剥離や旋回流などは苦手ですが、安定性があり、また計算時間が比較的短いなどのメリットから使用されることが多いようです。全体的なパターンを把握するのであれば、適切な選択といえるのかもしれません。

　ただし、k-εモデルといっても、「高Re数モデル」や「低Re数モデル」、さらに剥離をより良好に予測する「RNG k-εモデル」などもあり、いずれにしても適切なモデルの利用には、“自分が何をしようとしているのか”という解析の目的とともに、各モデルの特徴を把握していることが重要です。

　また、1つ言えるのは商用ソフトによって実装されているRANSの乱流モデルはさまざまで、“万能な、あるいは普遍的な乱流モデルはない”ということです。乱流モデルに限らず、このあたりのさじ加減一つで解析結果も変わってくるというのが流体解析の難しいところだと、構造解析ともどもやっている筆者は身をもって感じております。