3σと不良品発生の確率を予測する「標準正規分布表」:3D設計推進者の眼(31)(2/4 ページ)
標準正規分布とは
正規分布の話をする上では、その平均値μの位置は、これまで使用した正規分布のようにY軸上にあるということはありません。実は、これまで使用してきたものは、「標準正規分布(Standard Normal Distribution)」といわれるものになり、「平均値μ=0、標準偏差σ=1、分散σ2=1、N(0,12)」いうものになります。
上の図には、非常に単純な正規分布のグラフを示しています。この標準正規分布のグラフの横軸は、標準偏差の何倍になるかを示しています。そういうことから、±1の区間では1倍、±2の区間では2倍、±3の区間では3倍となります。
しかし、実際に正規分布になるヒストグラムをグラフ化すると、下図のようになるのではないでしょうか。
不良率を求めるためには「標準正規分布表」を使用します。標準正規分布表は「標準正規分布においてその値以上の値を取る確率」を示しています。くれぐれも、標準正規分布であることに注意してください。
標準正規分布のグラフを示しましたが、このように横軸には寸法などの変数、縦軸には確率密度が記載されているものに対して、横軸上の任意の値を規格値として「Kε(ケイ・イプシロン)」として、このKεを外れる、すなわちこのKεのグラフの外側になる確率を示した「ε(イプシロン)」を、標準正規分布表から求めることができます。この標準正規分布表ですが、Web上でもいろいろな場所で公開されていますが、自分でExcelを使って作成することも可能ですので、試してみてください。
例としては「Kε=1.11」とすると縦軸の0.1刻みの数値と、横軸の0.01刻みの数値の交差する位置から、「ε=0.133500」となり、1.11以上という数値になる確率は「0.133500」という数値を読み取ることが可能で、よって「13.35%」ということが統計学的に推測できます。
実際に測定した値は、この標準正規分布ではありません。しかし、平均値からのσの大きさに応じたデータの存在する確率は同じであると話しました。このことから、標準正規分布ではない分布からも、「統計学的にある規格値Kεを外れる確率εを推測することは可能」だということになります。これを行うために「正規分布の基準化」を行います。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
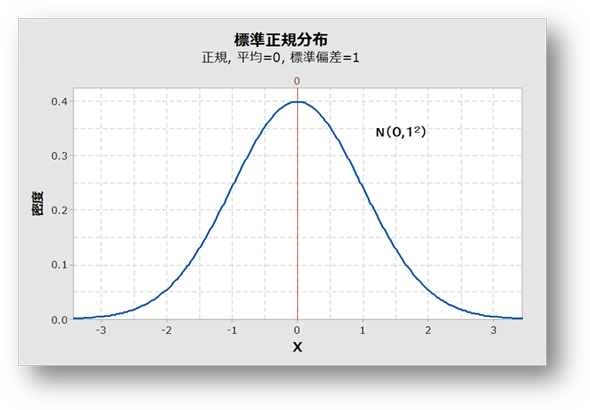 標準正規分布のグラフ(構造計画研究所Minitab17で作成後編集)
標準正規分布のグラフ(構造計画研究所Minitab17で作成後編集)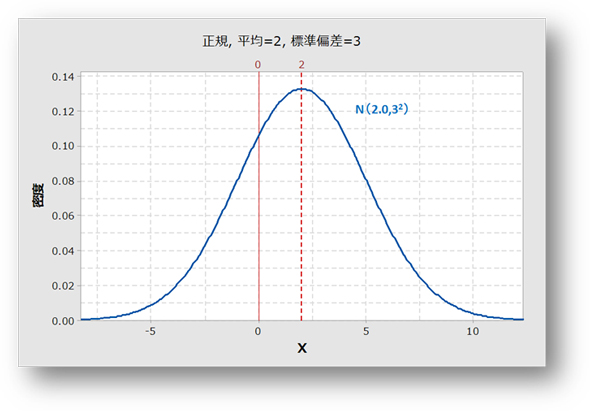 実際の正規分布(構造計画研究所Minitab17で作成後編集)
実際の正規分布(構造計画研究所Minitab17で作成後編集)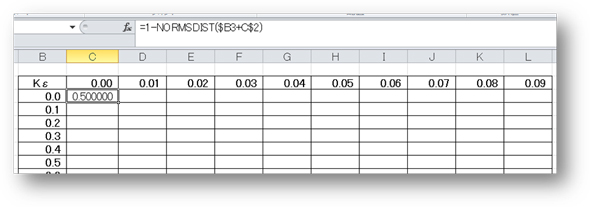 NORMDIST関数を利用して規格値を外れる確率を計算Kε≧0(Excel使用)
NORMDIST関数を利用して規格値を外れる確率を計算Kε≧0(Excel使用)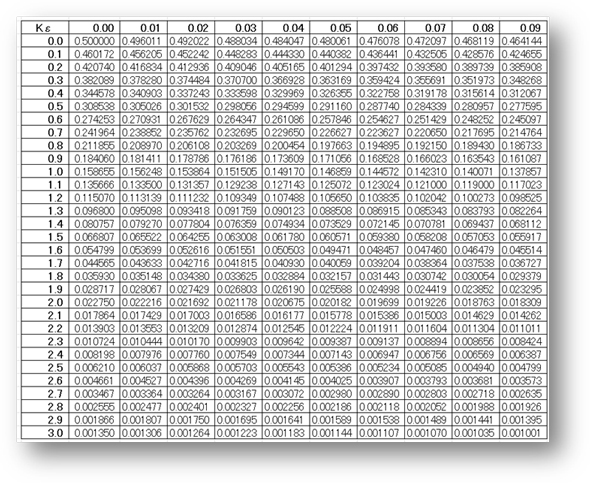 標準正規分布表から規格値を外れる確率の表を作成、Kε≧0 (Excel使用)
標準正規分布表から規格値を外れる確率の表を作成、Kε≧0 (Excel使用)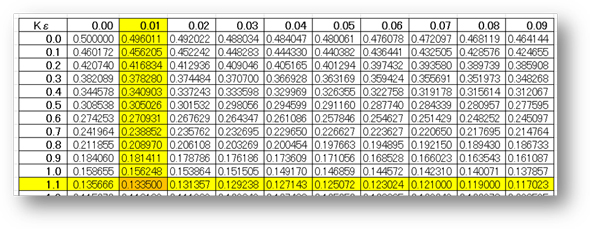 標準正規分布表からεを求めるKε≧0(Excel使用)
標準正規分布表からεを求めるKε≧0(Excel使用)





