3σと不良品発生の確率を予測する「標準正規分布表」:3D設計推進者の眼(31)(3/4 ページ)
正規分布の基準化とは
前述の内容から、実際に任意の平均値μと標準偏差σの正規分布を標準正規分布に変更する基準化という作業が必要になります。
語句の定義の再確認と設定をします。
- 標準正規分布N(0,12)における規格値(上限規格値):Kε
- 標準正規分布N(0,12)における規格値(上限規格値)を外れる確率:ε
- 平均値:μ
- 標準偏差:σ
- 平均値μ、標準偏差σの正規分布N(μ,σ2)における規格値(上限規格値):x
これらのパラメータにより、基準化の手順を次のように示します。
この作業について、グラフを見ながら考えてみましょう。
平均値μをx=0の位置に合わせるため、μ( μ ≧ 0 の時)の大きさ分、左にスライドさせます。従って、上限値xはx−μとなります。次に、任意の標準偏差σを標準偏差σ=1に変換します。
このためには、標準分布を任意の標準偏差 σ で割り算する必要があります。これにより、標準正規分布の所でお話した横軸が示す寸法などの変数のそれぞれが、σの何倍かということを表現できることになります。
このような手順で、正規分布の基準化ができます。またこの基準化により標準正規分布表からの、上限規格値Kε超える不良率が統計的に予測できるようになったわけです。
さて、このように上限規格値Kεを超える不良率を求めることができたということは、「公差計算・公差解析において、どのようなことができるようになったのか」という予想ができることでしょう。
「上限規格値Kε」としましたが、上限規格値をU、下限規格値Lとしたらどうでしょう。
そうです。例えば、平均値μを中心値とするような場合、「設計者が寸法公差を決める場合、統計学的にこの寸法公差を超える(外れる)確率を推測することが可能になる」ということになります。
前回使用したモデルをベースに考えてみます。この測定結果は仮想の実測データでしたが、あらたに同じものを作る時に、この上限規格値U=10.2[mm]を超える確率を求めてみます。
中心値としてμ=10[mm]、前回の標準偏差よりσ=0.08159とします。この時のKεを計算します。
- Kε=(10.2−10.0)/0.08159=2.45
- (標準正規分布表から)ε=0.007143
従って0.7%となり、「1000個作ると、7個上限規格値を超える可能性がある」ということが推測できました。
このような考え方は、「定められた規格値、すなわち公差範囲内でいかにものを作ることができるのか、組み立てることができるのか」を検証するということにつながっていきます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
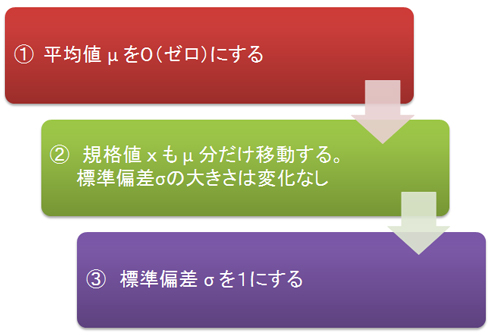 正規分布の基準化
正規分布の基準化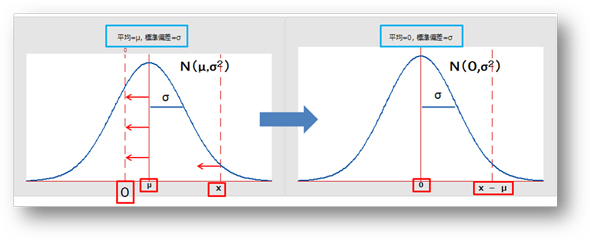 1:平均値を0(ゼロ)にする、2:標準偏差σの大きさに変化はなし(構造計画研究所Minitab17で作成後編集)
1:平均値を0(ゼロ)にする、2:標準偏差σの大きさに変化はなし(構造計画研究所Minitab17で作成後編集)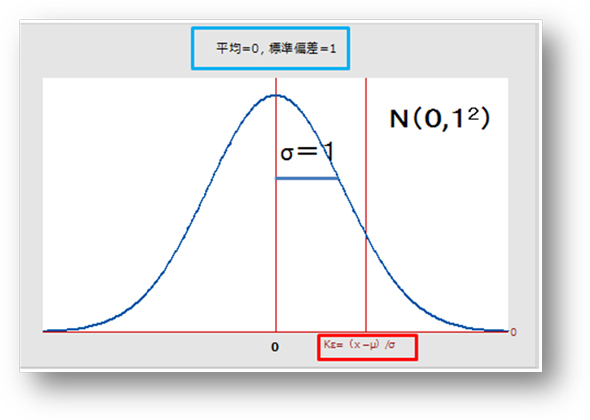 3:標準偏差を1にする(構造計画研究所Minitab17で作成後編集)
3:標準偏差を1にする(構造計画研究所Minitab17で作成後編集)
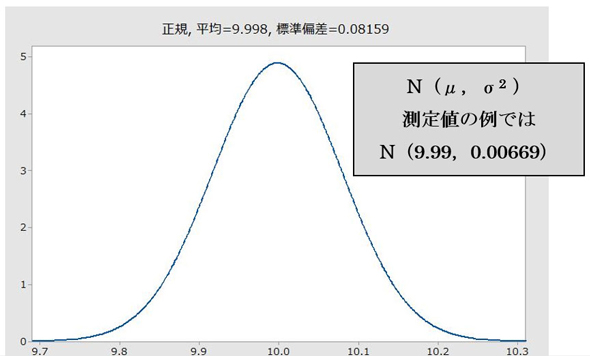 前回使用モデルとその測定値の正規分布(SOLIDWORKSと構造計画研究所Minitab17で作成)
前回使用モデルとその測定値の正規分布(SOLIDWORKSと構造計画研究所Minitab17で作成)





