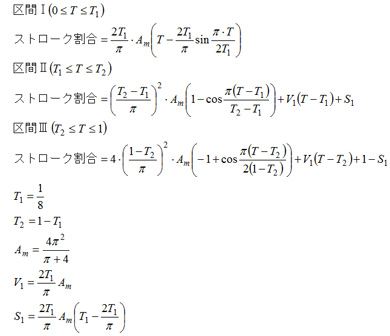　例えば、上端あるいは下端では、カム表面への力が下向きに加わるとすれば、法線の向きは半径方向のため、両者は一致し、圧力角は0となります。一方、上昇・降下部分では、図2に示すように、カム表面への力の向き（この場合横向きに表示）と、破線で表示したカム表面の法線方向とは、一致せず、ある角度を成します。これが圧力角で、圧力角が大きいと、カム表面の接線方向には摩擦力以外の力が加わり、カムへの負荷トルクの増大やカムの損傷を招きます。

　一般に、ロッドが上下する直動型のカムでは、圧力角は30度以下に、また、レバーが搖動する搖動型のカムでは、圧力角は45度以下となるように設計します。また、無次元最大速度は後述するカム曲線固有の値です。

　（6）式から分かるように、カムの大きさはストロークに比例し、割付角に反比例します。従って、上昇・降下時間の割合を小さくすると、カムは大きなものになります。

　例えば、最大圧力角30度、無次元最大速度が1.76（後述のMS曲線の無次元最大速度）としてカム有効径を求めると、カム有効径は約34mmとなります。ストロークは10mmであるため、半径34－10／2の円弧と、半径34＋10／2の円弧とを、直線的に半径が変化する円弧でつなぐと、カム形状が求められます。このようにして作図した形状が図2のカム形状です。

　図2の形状でも、取りあえずは機能しますが、下端・上端と上昇・降下部分とのつなぎ目が不連続となっていて、この部分でロッドやレバーが滑らかに動作しない恐れがあります。そこで、つなぎ目の部分が滑らかに接続されるようにした曲線がカム曲線と呼ばれるものです。カム曲線には複数の種類があり、用途により使い分けますが、最もオーソドックスなものが、下記のMS（Modified Sine：修正正弦）曲線です。

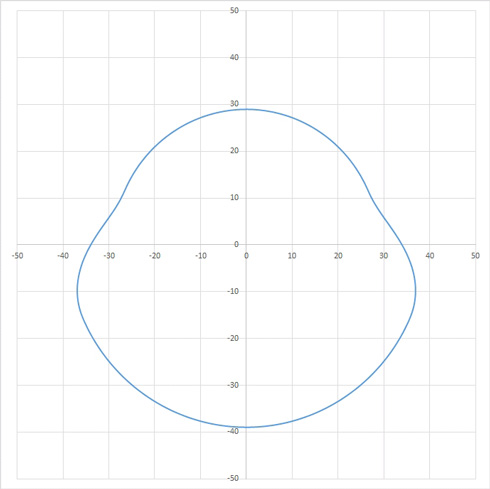
　図2と同じ条件でMS曲線を用いて設計したカムが図3に示す形状です。

図3：MS（修正正弦）曲線を用いたカム形状

　図3を見ると、下端・上端と上昇・降下部分とのつなぎ目が滑らかにつながれていることが分かります。カム曲線では、割付角内を0~1に配分し、対応する変位を0～1の無次元化された値で表現します。従って、カム曲線を利用するには、実際の角度から、変数Tを求め、対応する区間のカム曲線式からストローク割合を計算します。得られたストローク割合とストローク最大値との積を求めるとストロークすなわち、下端からの相対変位量が得られます。