主人公なのに影が薄い位置度と、とにかくキョーレツな輪郭度：寸法を実感する！ 測定講座（5）（3/4 ページ）

[木下悟志／プラーナー，MONOist]

主人公のはずだが認知度が低い、位置度

　次に位置公差の主人公といえる、位置度ですが、これは以前から幾何公差を目にしたことのある人の中でも意外に認知度の低い公差です。ですが、今後幾何公差の普及に伴って、次に述べる輪郭度とともに主役として一気に一般化してくるはずです。この公差はその名の通り、対象となる形体のデータムからの位置を規制するもので、そこには平行度、直角度、傾斜度、などの姿勢公差、さらには同軸度の代用もできるなど、ここまで見てきた幾何公差を包含した機能を持っています。対象とする形体も、部品の表面となる形体に加え、中心平面、中心軸などの誘導形体にも適用できる便利な幾何公差です。

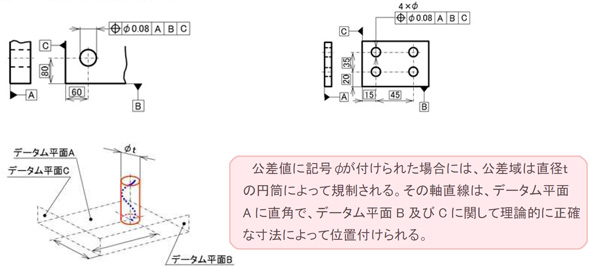
　位置度を規制するためには「真位置度理論」という考え方がありますが、要は位置を表す寸法には理論的に正しい寸法として□で指示して（寸法値を四角い枠で囲う）、その位置に関する公差は公差記入枠に指示をします。しかも、複数ある形体には1カ所の指示にまとめることで図面がスッキリします。図3に代表的な位置度公差として穴位置の規制に用いた例とその公差域を例示します。

図3：穴位置への位置度の適用事例

　穴位置に位置度を適用する場合はこの例のように公差域にΦで示した円筒公差域を用いる例が圧倒的に多くなります。

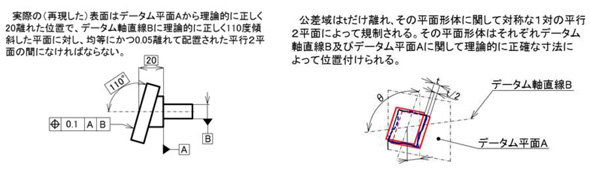
　図4は傾斜した面への位置度の適用事例です。

図4：傾斜面への位置度の適用事例

　公差域が先に出てきた傾斜度によく似ていますが、ここでは位置公差なので、傾斜度が角度110°のみを規制していたのに対して、データムAからの20という距離とデータムBに対する110°の角度の両方に対して規制しています。しかも、ここにデータムの優先順位があるので、測定に際しては実際の部品と設計形状（設計モデル）との位置合わせをするのに、まずデータムAを合わせ、次にデータムBを合わせることまで明確に指示しています。これは、測定上の意図のみでなく、組み立てする際に、実際にこの順で相手部品との合わせを行う可能性もあります。または、この部品が回転する部品である場合に、回転の変動の規制を回転軸であるデータムAよりも、受面であるデータムAでの規制を優先した設計になっている可能性が大きいことが想像されます。それこそが、まさに設計意図なのです。幾何公差では、こういった設計者の意図が明確に読み取れるはずです。もちろん設計者はそれを最大限に意識して設計し、製造側の人は、製造上の工夫や測定の安定性などを反映するように、お互いによく連携することが大切です。