主人公なのに影が薄い位置度と、とにかくキョーレツな輪郭度：寸法を実感する！ 測定講座（5）（2/4 ページ）

[木下悟志／プラーナー，MONOist]

同軸度と対称度は同じ概念

　まず、皆さんにもおなじみの同軸度ですが、これは説明するまでもなく、公差の記号から想像できるように円形形体同士の中心軸の位置関係に対する規制であり、JISの定義では「データム直線と同一線上にあるべき軸線のデータム軸直線からの狂いの大きさ」となっています。ここで、同心度と何が違うのかという疑念が生じると思いますが、同心度と同軸度は限りなく同義で、同心度が任意の断面または厚み方向の考慮の不要な薄い部品に適用するのに対し、同軸度は厚み方向も考慮する必要のある部品に適用することの違いだけです。一般的には、同軸度を適用することになります。ですから、JISの分類表では区別していますが、私どもの分類表（図1）では同軸度、同心度は同じものとしてまとめています。

　ここでは、同軸度と対比して「対称度」を紹介します。対称度は、世間ではなじみの薄い公差で、その名前から誤解をされているケースも多いのです。その名前から、中心軸や中心平面に対して関連する両側の形体同士の形状精度のように思われていることが多いのですが、この定義もJISでは、「データム軸直線またはデータム中心平面に関して互いに対称であるべき形体の対称位置からの狂いの大きさ」とされ、実は同軸度とほとんど同じ概念なのです。つまり、円形形体同士ではなく、角形状の中心平面や、円形形体同士でも直交方向である形体の中心位置に関して規制できるので、広義では同軸度もこの中に含まれます。

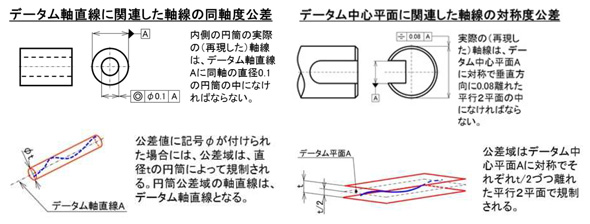
　分かりやすい対比として、図2に同軸度と対比しての図示例を並べて示します。

図2：同軸度、対称度の比較（似たもの同士）

　左の同軸度は円筒の中心軸をデータムAとし、内側の穴の中心軸の位置をΦ0.1mmの円筒公差域の範囲に規制します。一方、右の対称度は、中心の切欠き形状の中心平面をデータムAとし、外形の円筒中心軸の位置を、幅0.08mmの公差域に規制しています。いずれも、誘導形体をデータムとして、公差指示対象形体の中心の位置を規制している点では同じです。