統計の食わず嫌いを直そう(その11)、5分で残存バグ数を予測する方法:山浦恒央の“くみこみ”な話(83)(2/4 ページ)
» 2016年03月24日 07時00分 公開
[山浦恒央 東海大学 大学院 組込み技術研究科 非常勤講師(工学博士),MONOist]
3.回帰分析とは
回帰分析とは、2つのデータの関係を「y = ax + b」という方程式に置き換えることです。こう説明すると、難しそうですが、基本的な考え方は、中学校で習った1次方程式(y = ax + b)と変わりません。例えば図.1のグラフです。
図.1は、散布図を用いたグラフです(*1)。散布図は、データ可視化手法の1つで、xとyの関係を把握できます。青点は「xとyの実際の関係」、赤線は「黒線との距離」、黒線は「赤線の長さの合計が最小になるように引いた線」です。
中学生時代、皆さんは先生が読み上げたいろいろな(x, y)の値から青色の点をプロットし、点に最も近い線を引くような宿題があったはずです。図.1で、青点から黒線に引いた赤線の長さの合計が最小になる黒線が、回帰分析で導出する方程式です。つまり、黒線が回帰分析の出力結果となります(*2)。
最小になる線の求め方は習わなかったでしょうが、やっていることは中学校の数学と同じです。この説明で理解できなかったとしても気にすることはありません。実際の作業は全てExcelのツールまかせです。
(*1)説明のため、意識的に原点を表示していません。
(*2)具体的な算出方法は割愛します。
図.1から離れ、求めた方程式を考えます。例えば、xをソースコード行数、yを残存バグ数として回帰分析で求めた方程式が、「y = 0.1x + 3」としましょう。テスト開始前の対象の行数が3000行だとすると、残存バグ数= 0.1*3000 + 3となり、残存バグ数が303個あることが分かります。
4.予測モデルの構築
では、実際に予測モデルを作りましょう。
関連記事
 統計の食わず嫌いを直そう(その10)、ワインを飲まずに品質を予測する方法
統計の食わず嫌いを直そう(その10)、ワインを飲まずに品質を予測する方法
統計アレルギーの解消には、身近な分野で考えてみることも大切です。今回は「ワインを飲まずに、ワインの品質を予測する方法」を例に統計に触れてみましょう。 統計の食わず嫌いを直そう(その9)、昼休みにタダで統計分析をする方法
統計の食わず嫌いを直そう(その9)、昼休みにタダで統計分析をする方法
「統計分析」と聞くと面倒な感じですが、何を証明するか明確ならExcelで簡単にこなせます。Excelさえあれば追加費用はかからず、しかもランチタイムに終わるほどカンタンなのです。 統計の食わず嫌いを直そう(その8)、統計的に「王様の耳はロバの耳」と言うために
統計の食わず嫌いを直そう(その8)、統計的に「王様の耳はロバの耳」と言うために
「王様の耳はロバの耳」と統計的に判定するには、どうすればいいのでしょうか?ロバの耳かも?という仮説を“検定”するための基本的な考え方を学びます。 統計の食わず嫌いを直そう(その7)、「鎌倉時代の平均ワイン消費量」と「平均値の検定」
統計の食わず嫌いを直そう(その7)、「鎌倉時代の平均ワイン消費量」と「平均値の検定」
「効果がある」と言うためには比較が必要です。新旧開発プロセスの生産性や品質の平均値を比べるためには、「平均値の差の検定」が必要となります。 食わず嫌いを直そう、朝顔の観察日記とデータ収集(その6)
食わず嫌いを直そう、朝顔の観察日記とデータ収集(その6)
難しそうな「統計」ですが、データの分析以上に重要なのが「収集」です。今回は、統計分析の前段階に相当する「データを集める」という部分に焦点を当てて解説します。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 出荷量1.3倍を実現、電源不要のIoTゲートウェイが南種子町にもたらす農業改革
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
Special SitePR
コーナーリンク
あなたにおすすめの記事PR
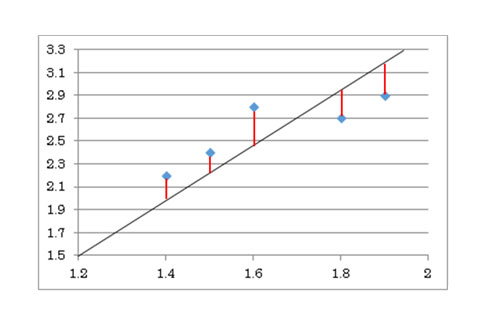 図.1 回帰分析と1次方程式
図.1 回帰分析と1次方程式

