統計の食わず嫌いを直そう（その9）、昼休みにタダで統計分析をする方法：山浦恒央の“くみこみ”な話（81）（2/3 ページ）

[山浦恒央 東海大学 大学院 組込み技術研究科 准教授（工学博士），MONOist]

2.　例題1：新人教育の効果検証

　次年度入社予定の新人に対し、E-learningで入社前教育を行いました。教育効果を評価するため、教育の前後でテストを実施し、結果を考察します（テストは100点満点。結果は表.1参照）。

表.1　E-learning前後のテストの点数
社員No	教育前(E-learning前)	教育後(E-Learning後)
1	50	54
2	84	89
3	78	84
4	61	77
5	94	91
6	99	100
7	45	56
8	73	78
9	38	55
10	80	78

2.1　仮説の設定

　「入社前のE-learningには効果があった」ことを統計的に証明したいので、それに沿った帰無仮説と対立仮説を設定します。

　帰無仮説と対立仮説については、前回のコラムでも解説しましたが、「王様の耳はロバの耳」であることを統計的に証明したい場合、無にしたい仮説、あるいは、否定したい仮説が帰無仮説で、「王様の耳は国民と同じである」という仮説です。対立仮説は、採用したい仮説、すなわち、「王様の耳はロバと同じ」になります。

「入社前のE-learningには効果があった」ことを証明したい場合、帰無仮説と対立仮説は以下のように設定します。

　・帰無仮説：入社前教育として、E-learningの効果無し

　・対立仮説：入社前教育として、E-learningの効果有り

　帰無仮説が無にならなかった場合、「入社前教育として、E-learningの効果無し」となり、教育手法を考えなおす必要があります。

2.2　データの分析

　データを整理・分析します。今回は、Excelの「分析ツール」内の「一対の標本による平均の検定」を使用します。よって、必要なデータは、E-learning実施前後のデータ（上記の表.1）があればOKです。

　Excelでの操作手順は次のようになります。

（1）「データ分析」から「一対の標本による平均の検定」を選択し、「OK」をクリックします。

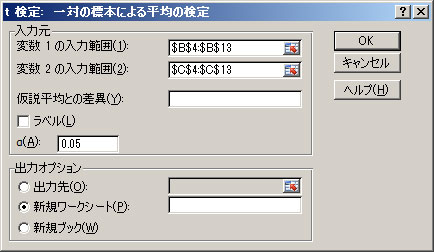
（2）データを挿入します。「変数１の入力範囲（１）」、「変数２の入力範囲（２）」に表.１のデータをそれぞれ入れ、「OK」を選択します。因みに、αを変更すると有意水準を変更できます(有意水準については、前回のコラムを参照。今回は５％なので0.05)。

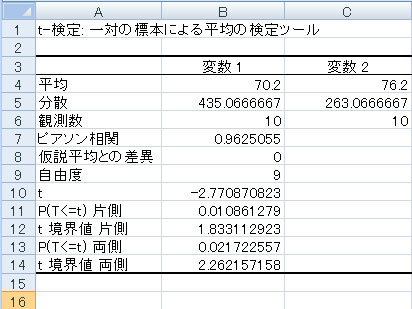
（3）結果が出ます。

　両側検定ですので（両側検定については前回のコラムを参照）、注目する部分は「検定量（P(T<=t)両側）」と、設定した「有意水準（α値）」です（今回のαの値は0.05です）。(t検定では、検定量はp値とも呼びます)なお、「（P(T<=t)両側）」の見方は以下の通りです。

• 「検定量(P(T<=t)両側)」 ＜＝ 0.05の場合、有意差有り
• 「検定量(P(T<=t)両側)」 ＞ 0.05の場合、有意差無し

　「P(T<=t)両側」は0.022ですから、0.022 <= 0.05となり、前後に差があることがわかります。結果として、「入社前の教育として、E-learningは効果がある」と判定できそうです。