原子炉施設の3次元FEM耐震解析のモデル化法を検討:CAE事例(3/3 ページ)
レイリー減衰の係数を新しく検討
要素別レイリー減衰は、要素質量マトリックスに係数αe、要素剛性マトリックスに係数βeが掛かった和となっている(図5)。
このαeとβeの値によって減衰の特性が変わる。そのため非常に重要だが、その決定方法についてはあまり研究が進んでいなかったという。
発表では、重み付き最小二乗法における値Jeが最小になるような、αe、βeを設定する方法を検討した(図6)。
使用したFEMモデルでは固有モードごとに減衰が違うため、これらは固有モードごとの設定となる。なお各固有モードにおける重み係数の付加を検討した。解析結果は入力の地震動のスペクトル特性と、対象モデルの応答特性の2つが大きく効いてくる。そのためこれらを考慮し、重み係数は応答スペクトルと刺激関数の積として設定した。
なお減衰比はそれぞれ、原子炉建屋、格納容器、遮蔽壁とペデスタルが5%、圧力容器と内部構造物が1〜7%である。
誤差範囲が従来法より小さいことを確認
この要素別レイリー減衰を用いた場合の解析結果と、比較のためにレイリー減衰を使用した従来研究(※1)における解析結果の最大絶対加速度を比較した(図7)。
入力波には地震を模擬した広帯域のランダム波を用いた。線形の時刻歴解析を実施した。解析モデルの全節点における最大加速度を計算して、その誤差を、ひずみエネルギー比例型減衰を用いた場合の解析結果を基準とした誤差を求めて評価した。ひずみエネルギー比例型減衰の場合は直接法では時間がかかるため、モーダル法を用いた。
その結果、従来研究の場合は最大50%程度の誤差率の広がりが出た。それに対して新しく開発した方法では、±20%の範囲に収まっていた。これより従来の方法よりも要素別レイリー減衰の方が有効だと分かった。場所により減衰は大きく変わるが、どの場所で見ても、各誤差率の分布は小さくなっていた。従って、新しく開発した方法で、減衰はある程度、正確に得られる見込みが得られた。今後はまだ残っている誤差をどう取り除いていくか検討を進めていくということだ。
関連記事
 「私の経験上」という言葉が出たら、ご用心!
「私の経験上」という言葉が出たら、ご用心!
災害を未然防止する設計をするために、問題解決理論のTRIZを適用して、常識にとらわれない視点での対策を立てよう。 日米ロボット、原子炉格納容器に通じる配管付近で高線量を計測
日米ロボット、原子炉格納容器に通じる配管付近で高線量を計測
東京電力は、原子炉格納容器の調査・補修工法の検討を目的に、福島第一原子力発電所 1号機 原子炉建屋内1階のパーソナルエアロック室の調査を実施。三菱電機特機システムの「FRIGO-MA」と米iRobotの「PackBot」を投入した。 「ASIMO」の技術を応用した「高所調査用ロボット」が原子炉建屋内で初仕事
「ASIMO」の技術を応用した「高所調査用ロボット」が原子炉建屋内で初仕事
ホンダと産業技術総合研究所(産総研)が東京電力 福島第一原子力発電所向けに共同開発した「高所調査用ロボット」が2013年6月18日、当初の予定通り、2号機 原子炉建屋内1階の上部空間の調査を実施。東京電力が調査結果に関する資料を公開した。 オールジャパンで挑む災害対策ロボット開発、実用化への道は?
オールジャパンで挑む災害対策ロボット開発、実用化への道は?
東日本大震災および東京電力・福島第一原子力発電所の事故発生当初、われわれに突き付けられたのは「日本の災害対策ロボットは実用レベルに達していない」という現実だった。あれから2年――。新エネルギー・産業技術総合開発機構(NEDO)の「災害対応無人化システム研究開発プロジェクト」の下、開発を進めてきた最新鋭の国産災害対策ロボット技術がプロジェクト完了を受けて一斉公開された。技術・運用面での課題はクリアできているのか? そして、実用への道は開けるのか? 原子力発電所をめぐる日米欧企業連合 vs. 韓国連合の戦い
原子力発電所をめぐる日米欧企業連合 vs. 韓国連合の戦い
脱石油エネルギーの1つとして注目を集める原子力発電。国を挙げての競争が激化する業界を知財マップで見てみると……
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

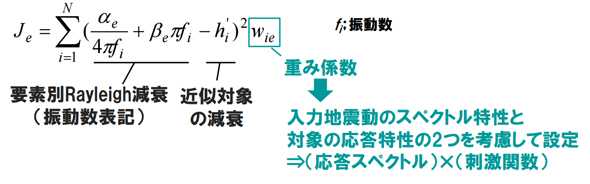 図6:減衰モデル化における計算式
図6:減衰モデル化における計算式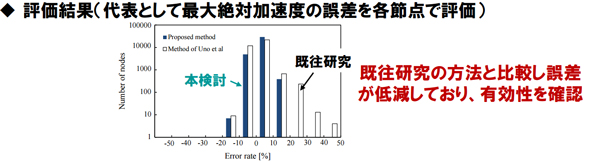 図7:減衰モデル化方法の検討結果
図7:減衰モデル化方法の検討結果






