生態系のバランスや、バタフライエフェクトの問題をODE45で解く:無償ソフトで技術計算しよう【シミュレーション応用編】(1)(2/2 ページ)
» 2015年02月23日 13時00分 公開
[伊藤孝宏,MONOist]
ローレンツ方程式
大気変動を研究していた気象学者のエドワード・ローレンツは、初期値のわずかな違いが気象の予測結果を大きく変えることに気付きました。これが、バタフライ効果と呼ばれているもので、下記のローレンツ方程式が、カオス研究の先駆けとなった式です。
では、ローレンツ方程式をFreeMatで解いてみます。下記のlorentz.mを保存し、コマンドウィンドウでlorentz(x初期値、y初期値、z初期値)と入力すると、図3に示すような結果が得られます。図3は蝶が羽根を広げたような形状で、ローレンツ・アトラクタと呼ばれています。
初期値を変えて計算してみると分かりますが、わずかな違いでアトラクタは形状を複雑に変化させます。参考までに、初期値を原点周りで半径0.1の円周上で変化させた場合のアトラクタの形状変化を動画にしたものを図4に添付しましたので、ご覧ください。
function lorentz(x0,y0,z0)
xyz=@(t,y) [-10*y(1)+10*y(2);-y(1)*y(3)+28*y(1)-y(2);y(1)*y(2)-8/3*y(3)];
span=[0,50];
t0=[x0;y0;z0];
[t,y]=ode45(xyz,span,[x0;y0;z0]);
plot3(y(:,1),y(:,2),y(:,3));
view(3);grid('on');
title(['X0=',num2str(x0),' Y0=',num2str(y0),' Z0=',num2str(z0)]);
xlabel('x');ylabel('y');zlabel('z');
axis([-30,30,-30,30,0,50]);
lorentz.m
初期値の違いによるアトラクタの変化
次回は振動問題をFreeMatで解いてみます。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
Special SitePR
あなたにおすすめの記事PR
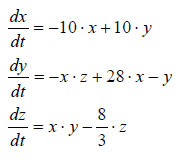
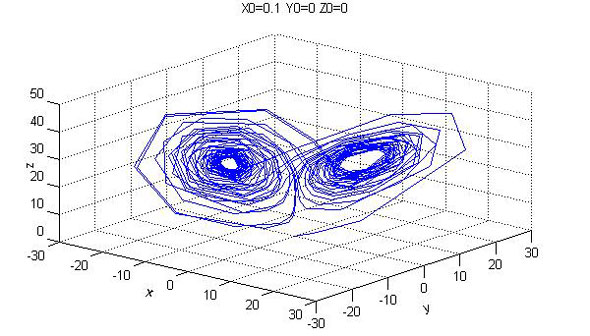 図3:ローレンツ・アトラクタ
図3:ローレンツ・アトラクタ






