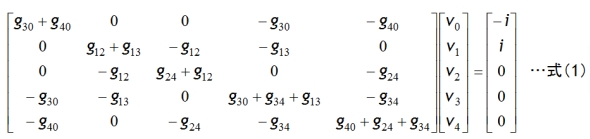節点法の計算原理を例題から学ぶ:SPICEの仕組みとその活用設計(2)(1/3 ページ)
第2回は、簡単な例題回路を使って節点法の計算を実際に行う。節点法の計算原理を理解するためにも一度は手計算で解いてみよう。
前回、最後に示した例題回路を図1に示します。今回は、この回路図上の全ての節点について、電圧と電流を省略せずに計算をしてみます。簡単な回路図なので、節点法ではなくΔ−Y変換を使った直並列計算だけでも解くことはできます。しかし、節点法の計算原理を理解するためにも一度は手計算で解いてみてください。筆を動かすことが理解の第一歩になります。頑張って、筆を動かしましょう。
例題回路の計算に入る前に、本連載の図や表、式の中に出てくる記号の表記法を次のように定めておきます。
- 小文字表記(g**、v**など)は、行列要素やベクトル成分、XY座標などの一連のデータ群を表します
- 大文字表記は、行列、ベクトルのような「概念」や、回路要素自体を指しますが、計算式中で使う場合は要素が持つ特性値を表します
- SPICEの統一規則に従い、節点番号0は接地電位に限定します
- 節点電位Viは、節点番号が小さいほど高いと仮定します。ですから、電流Iijは、節点番号の小さい方から大きい方へ流れる向きを正として計算式を記述します(もし、電位が逆転していれば電流の方向も逆転します)
- キルヒホフの電流則(電流バランスの式)は、本来の「電流の総和=0」を変形し、「流出電流=負流入電流」と考えて、“流出電流”−“流入電流”=“印加電流”と表現します
それでは節点ごとに、上記のルールに従って記述していきます。
注:ここでは抵抗値Rの代わりに抵抗の逆数であるコンダクタンスGを使います。理由は後述します。
節点1
印加電流:I(外部電流源I1より)
流入電流:0
流出電流:I12、I13
I12=(V1−V2)×G12、 I13=(V1−V3)×G13
I12+I13−0=I
∴(V1−V2)×G12+(V1−V3)×G13=I
節点2
流入電流:I12
I12=(V1−V2)×G12
流出電流:I24
I24=(V2−V4)×G24
∴I24−I12=(V2−V4)×G24−(V1−V2)×G12=0
節点3
流入電流:I13
I13=(V1−V3)×G13
流出電流:I30、I34
I30=(V3−V0)×G30、 I34=(V3−V4)×G34
∴I30+I34−I13=(V3−V0)×G30+(V3−V4)×G34−(V1−V3)×G13=0
節点4
流入電流:I24、I34
I24=(V2−V4)×G24、 I34=(V3−V4)×G34
流出電流:I40
I40=(V4−V0)×G40
∴I40−I24−I34=(V4−V0)×G40−(V2−V4)×G24−(V3−V4)×G34=0
節点0
印加電流:−I(外部電流源I1へ戻る電流)
流入電流:I30、I40
I30=(V3−V0)×G30、 I40=(V4−V0)×G40
流出電流:0
∴0−I30−I40=−(V3−V0)×G30−(V4−V0)×G40=−I
これらの式の係数を表1にまとめます。印加電流±Iは右辺にまとめます。
この表1を参考にして、前述した方程式を行列で書き表すと、
となります。また、式(1)は式(2)のように表記することもあります。
注:電位成分[V]、電流成分[I]は行列要素の1列分ですからベクトルといいます。各要素は表記法に従って小文字にしています。
次に、各要素の値について見ていきます。
行列[G]の各要素は回路の定数のみで成り立っているので、値については回路定数を決めた時に決まっています。
電流ベクトル[I]の各成分も各節点で印加/吸収がないとすれば、各項の成分を“0”に、印加/吸収があればそれぞれの値を各項に設定します(キルヒホフの電流則)。ですから、電流の各成分についても値は当然決まっています。
決まっていないのは各節点の電位ベクトル[V]ですが、行列[G]が正則*1)であることから、式(3)のように行列[G]の逆行列を左から掛けてやれば電位ベクトル[V]を求めることができます。
*1):[G]は正方かつ非0ですので正則行列です。正則行列でないと逆行列は存在しません。
Copyright © ITmedia, Inc. All Rights Reserved.
Factory Automationの記事ランキング
- 1.1秒に1個のブレーカー、4万の品番 パナソニック電気の見張り番のモノづくり
- 「ロボットが主役になる必要はない」ヒト型ロボット国内パイオニアの哲学と挑戦
- 工場を“ひらく”イトーキの共創拠点始動、新ワークチェア「SHIGA」開発秘話
- ヤマ発は2026年の関税影響額が3倍に、コスト構造改革で米国事業立て直し急ぐ
- ドイツの生産拠点に訓練施設開設、DMG森精機が人材育成を強化
- DMG森精機「受注の回復鮮明」データセンターなどけん引、BXで市場取り戻す
- “熟練作業者の目”を再現 中堅製造業向けの状況認識AI「メニナルAI」とは何か
- 「高市演説を受けて〜危うい現状認識〜」にズバリ書かれていたこと
- ベトナムに新たな金属加工拠点、単品から中ロットまで対応
- 「今後数年は伸びる」ソディックはデータセンター関連好調、発電関連で大型機も
コーナーリンク
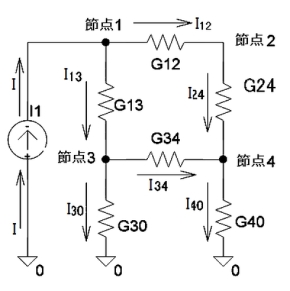
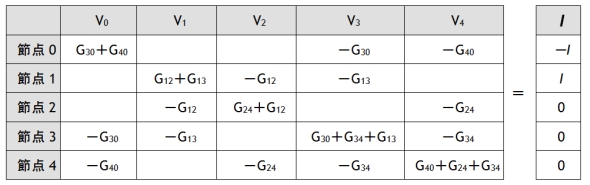 表1 各変数の係数一覧表
表1 各変数の係数一覧表