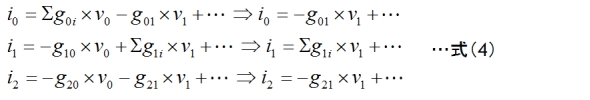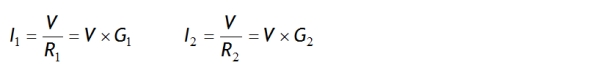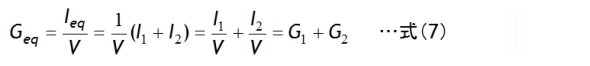節点法の計算原理を例題から学ぶ：SPICEの仕組みとその活用設計（2）（2/3 ページ）

[加藤博二（Sifoen），MONOist]

行列の構成

　次に、行列の構成について見ていくと以下のようなことが分かります。

• 各部品G_ijが接続される2つの節点番号（i,j）が示す、行列要素（i,j）,（j,i）にはそれぞれ関係するコンダクタンスの極性反転の値が入ります
• 各節点番号の対角要素（i,i）,（j,j）には、関係する要素のコンダクタンスの総和が入ります
• 対称行列です
• 疎行列ではありません（対角中心に行列要素が集まってはいません）

　例えば部品G₁₃の場合は関係する節点は1と3ですから、

• 行列要素（1,3）,（3,1）には、極性反転の−G₁₃が入り、
• 行列要素（1,1）,（3,3）には正のG₁₃がそれぞれ和の形で入る

という形で構成されていることが分かります。

　このようにして構成された行列ですが、実際の回路図では大地、すなわち、節点番号0の電位を0Vとし、他の節点との電位の差分を電圧として表しています。つまり、［G］［V］＝［I］の式中で、v₀を0Vとしているのです。ですから、v₀に関係する項は係数がどのような値でも結果が0になり、式（4）のように方程式から消去されてしまいます。

　このままでは、行列は1列目（v₀の列）が抜かれ、n行と（n−1）列の不正則の行列になり、解くことができません。

　しかし、ここで扱っている行列［G］は、もともと連立方程式の係数に起因したものですから、元の方程式に戻って考えると、i₀はv₀〜v_nを変数とした関数F（v₀、……v_n）になっていることが分かります。

　ここで、関数F（v₀、……v_n）は1次線形方程式なので、v₀とv₁〜v_nの項に分離でき、式（5）のように書き表せます。

　式（5）で、変数v₀の値を0に決めたということは、Kの値は回路構成やv₁〜v_nから既に決まっていますので必然的にi₀が決まることになります。そして、係数の決まっている方程式ではi₀、v₀の2変数を同時に規定できないことを思い出してください。

　これらのことから、i₀については解く必要がなく、i₀の行は行列［G］から削除できます。

注：i₀の値は0ではなく、他の計算結果から決まるということです。

　故に、行列は0行と0列を抜いて解けばよいことになり、正則を維持できます。図1の例題回路では、解くべき行列［G］は行列要素（1,1）〜（4,4）の4行4列になるのです。

要求精度

電圧（V）	0.1μV〜10KV＝10−7〜104
電流（A）	1nA〜1KA＝10−9〜103
抵抗（Ω）	1μΩ〜1GΩ＝10−6〜109
容量（F）	1pF〜1F＝10−12〜1
インダクタンス（H）	1nH〜100H＝10−9〜102
表2　電気回路の計算に用いる主な数字の有効桁数目安

　ここで、電気回路の計算に用いる精度の目安を表2に簡単に記しておきます。製品分野によっては使用する範囲が異なりますので、一例としてお考えください。

　表2の組み合わせを考えると最低でも10⁻¹⁵以上の精度を要求されることが分かります。このような高精度で、かつ非疎である行列［G］の解法としては、CG法に代表される反復法より直接法の方が安定して解を求めるられます。ちなみに、行列解法としてはガウスの消去法などがありますが、行列を解く手順は今回の連載の目的ではありませんので解法手順までは説明はしません。

　表計算ソフトでShift＋Ctrl＋Enterキーを使って、MINVERSE関数で解けることを理解していれば十分です。

抵抗とコンダクタンス

図2　並列回路（クリックで拡大）

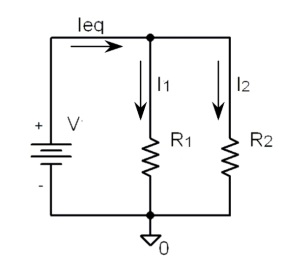
　皆さんが学校で習ったように、電流はI＝V／Rというオームの法則で計算します。しかし、この形で並列接続を表現すると、次に示すように式が複雑になってしまいます。

　図2のR₁とR₂の並列抵抗値R_eqは、よく知られている式（6）から求められます。

　このように、並列接続は等価抵抗を求めるために、乗除算を行わなければなりません。実際の回路においては、L、C、半導体のように複数のデバイスで構成される等価回路が存在し、ベース−エミッタ間やコレクタ−エミッタ間ごとに、何回もこの乗除算を繰り返して要素行列［G］を作り出さねばなりません。必然的にアルゴリズムが複雑になり、誤差も累積してきます。

　そこで、行列の組み立てを容易にするために、抵抗値の逆数であるコンダクタンスG（＝1／R）というパラメータを用いることにします。単位は“S”（ジ−メンス）です。このコンダクタンスとは、電気的に言えば“電流の流れやすさ”の値であり、材料力学的に言えば“力の伝えやすさ（剛性）”を示す物性値に該当します。

　このGの概念を用いて並列抵抗を表記すれば、図2の回路網は、

になります。そして、並列抵抗Reqに相当する合成コンダクタンスG_eqは、コンダクタンスの定義式（G＝I/V）から、式（7）のように単純にコンダクタンス同士の加算だけで計算できます。

　この機械的な簡便さが行列［G］を構築するアルゴリズム上では重要なのです。