ピンポン球を使って6自由度について説明してみた:設計者CAEを始める前にシッカリ学ぶ有限要素法(4)(2/3 ページ)
2.精度の補佐役 中間節点
部品の変形は有限要素の節点の変形で表されます。節点の変形量を「節点の変位(へんい)」といいます。有限要素の頂点には節点があります。節点そのものが変位します。要素内部の任意の点の変位は、要素の頂点の節点の変位から近似計算されます。その関数を「形状関数」といいます。
要素内部の任意の点の計算は、要素の構成節点が多いほど精度が上がります。要素の頂点の節点と節点の間に設けられる節点を「中間節点」といいます。
中間節点の数によって要素の精度は上がっていきます。中間節点が1つもない要素を「1次要素」といいます。そして、中間節点が1つある要素を「2次要素」といいます。それでは3次要素はあるのでしょうか? ……あります。ただし、一般的な有限要素解析で使う要素は2次要素までです。
一般的な設計者向けの有限要素法のソフトでも1次と2次の要素は普通に使えますが、3次要素となると、僕は見たことがありません。
さて、図4ではシェル要素の四角形を例に挙げましたが、三大有限要素すべてに1次要素と2次要素があります。もちろん3次要素もありますが、設計者向け解析ソフトでは見たことがないので、ここでは2次要素までとして、説明を進めます。
バー、シェル、ソリッド、それぞれの1次要素と2次要素を次の表にまとめました(図5)。
どの要素も2次要素がゆがんでいるように描かれています。中間節点は要素の頂点と頂点を結んだ直線の中間点にある必要はないのです。よってこのようにゆがんだ要素も表現することが可能です。
「ゆがんだ」というと言葉のイメージが良くないですね。これはつまり「要素の形状が柔軟である」ということです。部品を要素分割する場合、1次要素を使うと、要素のエッジが直線なので、部品に曲面がある場合、部品の形状を正確にトレースできません。例えば穴の形状をできるだけ正確に表現しようとすると、どうしても要素数が多くなってしまいます。2次要素であれば、1次要素よりは部品の曲面部分をより正確に近似することができます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
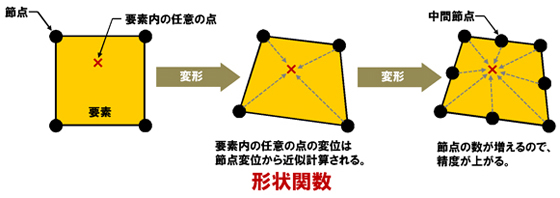 図3 要素内の任意の点の変位を決める形状関数
図3 要素内の任意の点の変位を決める形状関数 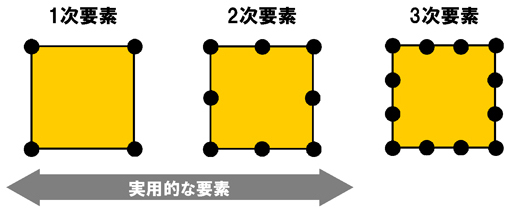 図4 要素の次数が上がると精度が上がる
図4 要素の次数が上がると精度が上がる 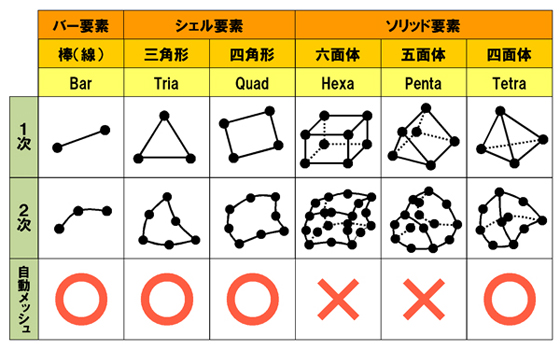 図5 三大有限要素と次数
図5 三大有限要素と次数 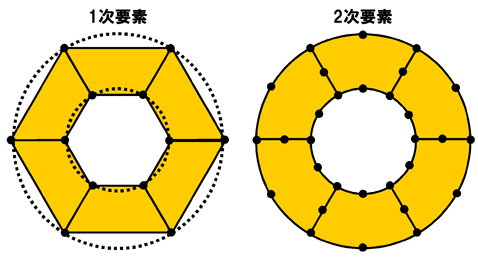 図6 部品の形状と要素の次数
図6 部品の形状と要素の次数 





