有限要素は、シャンパンの栓(せん)なのだ:設計者CAEを始める前にシッカリ学ぶ有限要素法(2)
メッシュ分割とは、有限要素を作ること。でも有限要素って何なの? コルク栓に例えて分かりやすく解説してみた。
正しい解析を行うためには、材料力学と有限要素法を知っておくことが大切です。前回の記事でそのことをお分かりいただけたでしょうか。
今回は有限要素法で部品や構造を表現するための「要素」について解説していきます。
1.部品は四面体のパズルだ
「有限要素法」。まずはこの言葉を分解してみましょう。
有限要素法=有限+要素+法
「有限」とは、いうまでもなく「限りがあること」です。「要素」は「カタマリ」ということにしておきましょう。そして「法」は「方法」の「法」。つまり「限りのある要素による方法」ということになります。有限要素法は、まず解析の対象となる「着目物体」をカタマリに分割することから始まります。着目物体とは、解析の対象となる部品などのことをいいます。
ここで1つ。解析の対象となる部品が、1つながりの部品ではなく、いくつかの部品が組み合わされたアセンブリということも、もちろんあるでしょう。一般的に、アセンブリでの解析は部品の解析に比べ難しいのです。特に部品と部品の接合部において、有限要素法特有の「仕掛け」を施す必要があります。アセンブリの解析については後ほど説明することとして、今回はまず、1つながりの部品について説明していきます。
1つながりの部品を「構造的に連続体である」といったりします。以下の図1は、ピストンを半分にしたものです。半分にした理由は、中が分かりやすいように。
実はそればかりではなく、「部品の形状も、部品に掛かるチカラも、部品の固定のされ方も対象であれば、その対象に応じてモデルを省略し部品を解析できる」というワザがあります。このことについても、後々、説明していきます。
このピストンは、四面体で分割されています。別の表現をすれば、
「いろんな形状の四面体が組み合わさって、部品のカタチを作っている」
ということができます。
小さい四面体もあれば、大きい四面体もある。細長い四面体もあれば、薄っぺらい四面体もある。カタチはさまざまですが、とにかく四面体が組み合わさって、部品のカタチを作っているのです。
そのうちの1つの四面体を取り出してみましょう。この四面体は、もちろん中が詰まっています。この四面体のことを「要素」、英語では「Element(エレメント)」といいます。この四面体の頂点を「節点」、英語では「Node(ノード)」。節点はATOKでさえも「接点」と変換してしまうので、注意しましょうね。「接点」ではなく「節点」です。
有限要素法を行うためには、解析の対象である部品を、上の図1のように要素に分割しなければなりません。これを「要素分割」といいます。要素分割されたものを「有限要素モデル」といったりします。さらに要素の分割を表す線が網の目状になることから「メッシュ分割」ともいいます。
このメッシュ分割、つまり有限要素モデル作成は、実は途方もなく大変な作業でした。解析全体の作業を100とすると、80はこのメッシュ分割に費やすといわれるほどでした。
なぜ“過去形”で書いたのか……。この作業は、現在ではまさに過去のモノとなってしまったからです。いまでは3次元CADのデータを基にして、メッシュ分割がほぼ「自動」で行われるからです。ただ「自動」とは「ブラックボックス」を意味します。
その中でどういうことが行われているのかは、次のページで説明していきます。
栗サンの「一休みコラム」
三角パックの秘密
四面体はとても面白い立体です。僕が小学生のとき、学校での昼ご飯は給食でした。牛乳瓶だった入れものがいつのころからか、いわゆる三角パックに変わりました。この三角パック、実は四面体なんです。
この三角パックには大きな2つの特徴があります。 その1つは、ロール紙を使って作る場合一切ムダな部分が出ないということ。そしてもう1つは四面体である三角パックは空間をすき間なく埋めつくせるカタチであるということです。冷蔵庫で冷やすにしても、運搬するにしても、ムダな空間がない方がいいに決まっています。三角パックの運搬ケースは六角柱で、ムダなすき間なく三角パックを詰め込めるようになっています。三角パックがムダなく収まる空間が六角柱。ハチの巣も六角形を基本にしています。なんか神秘的ですね。この「空間をすき間なく埋められる」という四面体の特性は、実は有限要素を自動分割ツールにも有効に生かされています。その特性について、詳しくは以下のURLを参照してみてください。かなり数学的な話ではありますが。
関連リンク:自己拡大する四面体
四面体のように3次元の要素を使っての説明は難しいので、さらに次元を1つ落とし、2次元で説明します。
縦30mm、横90mmの金属板を部品とし、それを解析の対象とします。これを要素分割していきましょう。要素分割は、要素をどれくらいの大きさにするか、などいろいろ迷うところではありますが、今回はカンタンにイメージするために、図2に示すように30mm×30mmの要素3つに分割します。
部品の形状をコンピュータの中でデジタルに表現するためには、節点や要素に番号を付けます。節点に付ける番号を「節点番号」、要素に付ける番号を「要素番号」といいます。
節点番号も要素番号も付ける数字は自由ですが、ここでは分かりやすくするために、節点番号は1桁(けた)で1から、要素番号は3桁で101から付けてあります。節点番号の重複は許されませんし、要素番号の重複も許されません。節点番号と要素番号で同じ番号があるのは許されています。
これでコンピュータの中に部品の形状を表現するための第一段階は終了です。
ここでは同じ大きさに要素分割しましたが、この要素の大きさとカタチそのものが有限要素解析の精度を左右します。要素の大きさやカタチはそれほど大切なことなのです。
2.部品の形状をコンピューターの中に再現する
ここまでは、節点と要素に番号を振って各節点と要素にIDを与えただけです。これだけではコンピュータの中に形状を表現することはできません。要素分割の状態はまだ表現されてはいないのです。
それでは早速、要素分割をデジタルで表現していきましょう。
まずは節点から。
節点は座標値で表します。座標値で表すためには、座標系が必要です。座標系はどこに取ってもいいのですが、今回は節点番号1を原点として、水平方向にx軸、垂直方向にy軸を取ります。そしてすべての節点をxとyの座標値で表します。節点1は原点と同じですので、「x=0,y=0」となります。この要領で、すべてのマス目を埋めてみてください。
次に要素です。
要素は「その要素がどの節点によって構成されているか」を表現します。要素101は、節点1→節点2→節点6→節点5で構成されています。ここで重要なのは、白い矢印のようにくるりと回るように、順番に並べるということです。例えば、節点1→節点2→節点5→節点6というふうに要素を表現すると、要素がねじれていることになってしまいます。“くるり”を守りながら、すべてのマス目を埋めてみてください。ちなみに“くるり”の方向は、時計回りでも反時計回りでも構いません。要素ごとに変わっていても構いません。
有限要素モデルの作り方というのは、基本的にこれにつきます。
どうですか、皆さん。メンドクサイでしょ? 要素の数はたったの3つ、そして節点の数は8つ。こんなに小さな有限要素モデルでも結構な手間が掛かることがお分かりいただけたと思います。解析で使う本格的なモデルは、大規模なものでは数十万要素というものがあるわけで、これを手作業で行うというのは、想像を絶するほどに手間が掛かります。さらにそれが3次元であれば、その手間はさらに膨らみます。図1の“ピストン半分モデル”程度でも、要素分割した四面体の各頂点の座標を節点として計算して、その節点をつなぐ、という作業は人力でやると膨大な時間が必要となります。ちなみに僕が駆け出しのころは、これくらいのモデル作成は手作業で10日くらいだったと思います。
栗サンの「一休みコラム」:こんな時代もありました
いまでこそ3次元CADのデータを使って効率的に要素分割をすることができますが、僕の若いころ、およそ四半世紀前は、この要素分割という作業が大変でした。当時の図面は、現在のようにCADでキレイに描かれているわけではなく、まだ手書きが主流で、「青焼き」と呼ばれる青写真をコピー代わりに使っていました。その上に鉛筆で要素分割のパターンを描き、節点の座標値を求めていきました。ワイシャツの袖口が鉛筆の粉で真っ黒になったのを覚えています。
しかも、グラフィックス機能のあるコンピュータがまだない時代。作成した要素分割に間違えがないかどうかのチェックがまた大変でした。いちいちペン・プロッターで要素分割図を出力し、チェックしました。要素分割の作成からチェックまで、現在の100倍以上の時間がかかっていたと思います。 「有限要素法は要素が大切」といいますが、このような経験をすると、その大切さが骨身に染みて理解できます。
3.シャンパンの栓(せん)が、要素のすべてを物語る
ピストンは要素を四面体で表現しました。要素のデジタル化の例題では、要素を四角形で表現しました。
要素にはいったいどのようなカタチがあるのでしょうか。そしてそれをどのように使い分けるのでしょうか。これは使用する有限要素解析ソフトによってさまざまですが、共通の概念も非常に多く存在します。一般的に、要素にはどのようなカタチがあるのか解説していきましょう。
要素のカタチは、シャンパンの栓に集約されています。図4はシャンパンの栓を分解したものです。
まずはシャンパンの栓(せん)を留めているハリガネ。棒状の要素で表現できます。次に、シャンパンのコルクを押さえているフタ。面積のワリに薄い板状ですね。これは板状の要素で表現できます。そして最後にコルク。これはボリュームのあるカタマリで中が詰まっています。
ハリガネのような棒状の要素を「はり要素」や「Bar要素」といいます。またフタのような板状の要素を「板要素」や「Shell要素」といいます。そして、コルクのようなカタマリ状の要素を「立体要素」や「ソリッド要素」といいます。
この3種類の要素の形態があれば、一般的な部品を表現することができます。もちろん、そのほかにもたくさんの要素がありますが、その中には特別な場合に使う要素もたくさんあります。有限要素法の“はじめの一歩”としては、まずはこの3種類を覚えておけば十分でしょう。
どれか1種類の要素をだけを使って有限要素モデルを組み立てるときもあれば、はり要素、板要素、ソリッド要素を1つの有限要素モデルの中で混在して使う場合もあります。
次回はこれらの要素の使い方について、もう少し踏み込んで解説しようと思います。(次回に続く)
関連記事
 材力とFEMをシッカリ理解して、シッカリ解析!
材力とFEMをシッカリ理解して、シッカリ解析!
小難しい有限要素法を数式を使わずに解説する。まずは有限要素法の歴史を振り返り、解析の基本的な考え方を確認。 ここからすべては始まる。三大有限要素はこれだ!
ここからすべては始まる。三大有限要素はこれだ!
「バー要素」「シェル要素」「ソリッド要素」のそれぞれが持つ長所や欠点を詳しく楽しく解説する。 ピンポン球を使って6自由度について説明してみた
ピンポン球を使って6自由度について説明してみた
ピンポン球が1個、箱の中にあって、天井からひもでぶら下がっている。実はこのピンポン球が有限要素の“何か”。 ソリッド四面体1次要素は、デンジャラス!?
ソリッド四面体1次要素は、デンジャラス!?
ソリッド四面体要素を使うときの、大事な約束がある。それを守らないと、危ない結果が待っている!? 超重要! メッシュサイズと8つの質問
超重要! メッシュサイズと8つの質問
解析精度を高めるため設計者自身でコントロールできる唯一のパラメータは、メッシュサイズだ。 3人中2人が間違える!? 片持ちばりの計算をしよう
3人中2人が間違える!? 片持ちばりの計算をしよう
今回は、これまでの解説内容を実践してみる。3人中2人が間違えるという片持ちばりの変形量計算にチャレンジ。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
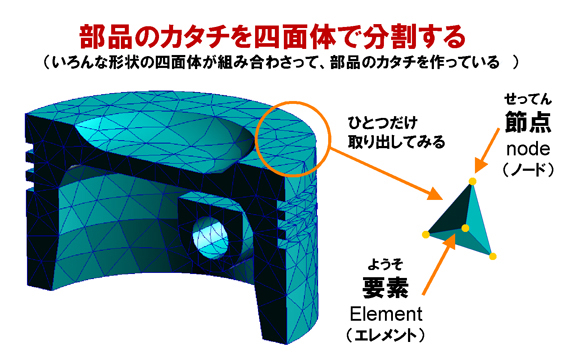 図1 ピストンを有限要素化してみた
図1 ピストンを有限要素化してみた
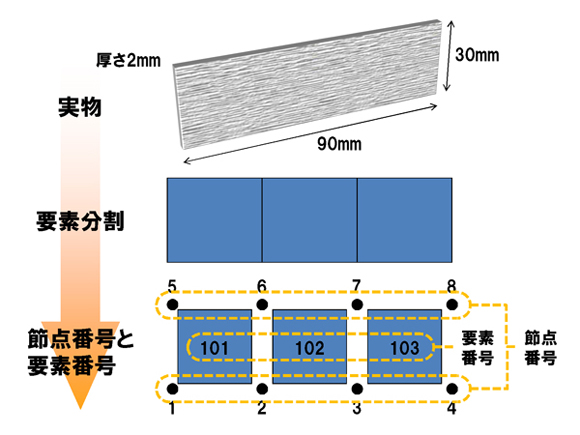 図2 節点番号と要素番号
図2 節点番号と要素番号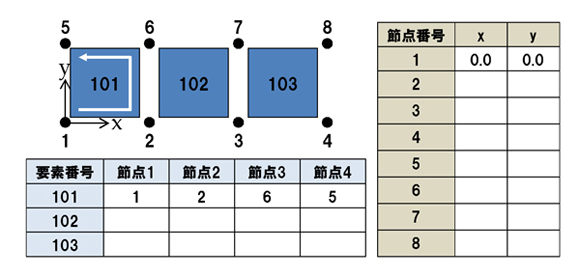 図3 要素分割のデジタル化
図3 要素分割のデジタル化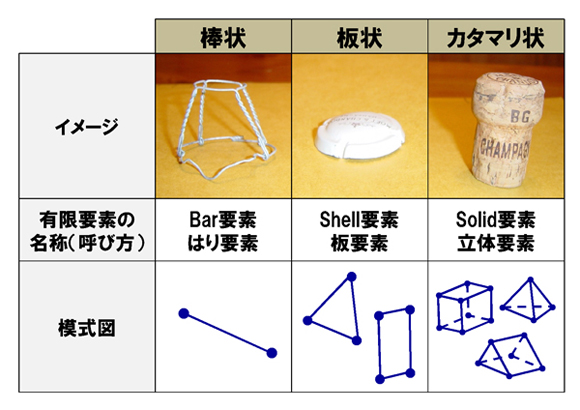 図4 シャンパンの栓の各部位と各要素
図4 シャンパンの栓の各部位と各要素 






