「日本は所得格差の小さい国」は本当か？ 所得格差を表す「ジニ係数」で見る：小川製作所のスキマ時間にながめる経済データ（35）（2/3 ページ）

[小川真由／小川製作所，MONOist]

ジニ係数の意味するもの

　前節の解説だけだと、イメージしにくいと思いますので少し腹落ちしやすい言葉と表現で解説を試みます。

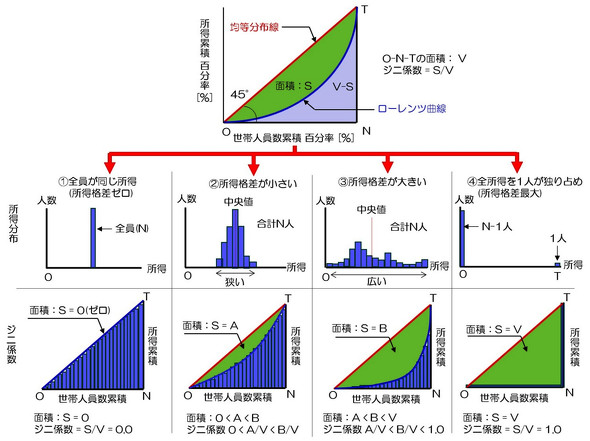
　ある集団について所得が低い順に並べた時の、所得累積値が描く曲線がローレンツ曲線となります。次の図2で示した4つのパターンで、具体的なジニ係数のイメージを固めてみましょう。

図2 タイプ別のジニ係数のイメージ［クリックで拡大］ 出所：筆者作成

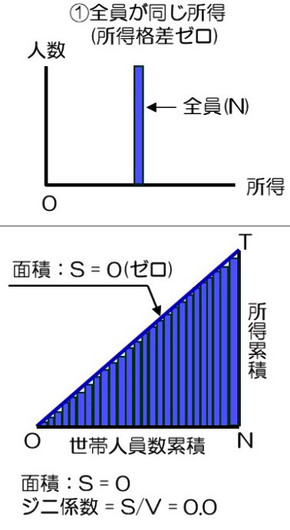
全員が同じ所得の場合（所得格差ゼロ）

図2-1 全員が同じ所得の場合［クリックで拡大］ 出所：筆者作成

　右の図2-1のような、全ての人が全く同じ所得の場合について説明します。全員が同じ所得ですので、所得格差はゼロです。中段の所得分布にあるように横軸に所得水準、縦軸に人数を取ると、この場合は全ての人がある所得に固まって分布していることになります。

　下段のように、横軸に世帯人員数の累積値、縦軸に所得の累積値を取ると、全員が同じ所得ですのでローレンツ曲線は45度の均等分布線に沿う形となります。この時均等分布線とローレンツ曲線で成す面積はゼロとなり、O-N-Tの面積Vとの比率もゼロです。つまり、全員が全く同じ所得=所得格差ゼロの場合は、ジニ係数もゼロという数値を取ることになります。

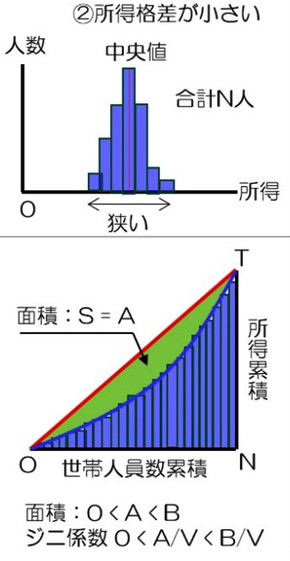
所得格差が小さい場合

図2-2 所得格差が小さい場合［クリックで拡大］ 出所：筆者作成

　図2-2のように所得分布が小さい状態をイメージしてみましょう。上段の図を見ると、この分布は、図2-1の所得格差がゼロの場合と比べると幅の広い分布となっています。一方で、図2-3の所得格差が大きい場合と比べると、中央値の近くにコンパクトに寄った分布となっています。つまり、多くの人が中央値付近の所得を得ていて、所得格差が小さい状況を示しています。

　この分布をローレンツ曲線で表現すると、下段のようになります。この場合、均等分布線とローレンツ曲線で構成される面積Sは、ゼロよりも大きく、図2-3の場合のBよりも小さくなります。つまり、O-N-Tの面積Vとの比率であるジニ係数を計算すると、A/Vとなり、これはゼロより大きく、B/Vより小さくなります。

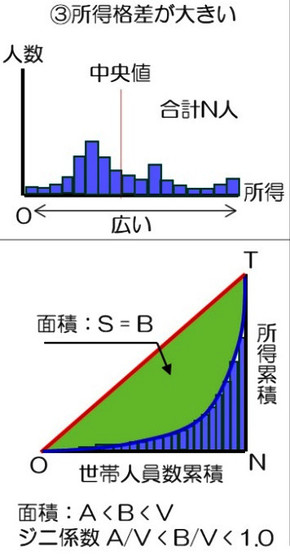
所得格差が大きい場合

図2-3 所得格差が大きい場合［クリックで拡大］ 出所：筆者作成

　図2-3は、図2-2の場合と同様ですが、所得が幅広く分布している場合です。上段の図を見ると、この分布は、低所得層と高所得層で所得水準に大きな差があるため、所得格差が大きいことを示しています。つまり、中央値からの分布の幅が広いことになります。

　この分布をローレンツ曲線で表そうとすると、低所得層を累積しても所得累積値はそれほど増えず、高所得層になるにつれて急激に立ち上がっていくようなグラフとなります。この場合、均等分布線とローレンツ曲線のなす面積は図2-2の場合のAより大きく、O-N-Tの面積Vよりも小さいことになります。

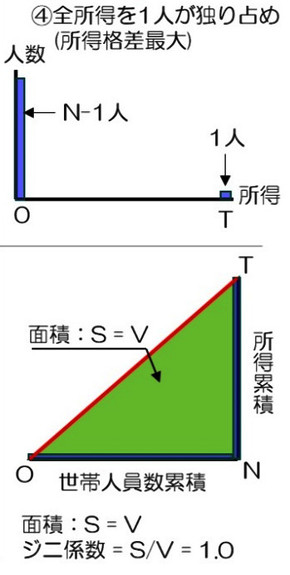
1人が所得を独占している場合

図2-4 1人が所得を独占している場合［クリックで拡大］ 出所：筆者作成

　集団の中で、1人が所得を独占していて、他の構成員の所得がゼロの状態が最も所得格差の大きい状態と言えますね。この場合のローレンツ曲線を考えてみましょう。

　N-1人目までは全てゼロですのでそれまでの所得累積値もゼロです、N人目で初めて所得Tが立ち上がるような形になります。

　つまり、ローレンツ曲線は直線O-Nと、N-TのL字に曲がった線として表現されることになります。均等分布線とローレンツ曲線のなす面積は、O-N-Tの面積そのもののVとなります。そして、面積Vとの比率はV÷Vで1.0となるわけです。

　このように、ジニ係数は所得格差ゼロの場合はゼロで、所得格差が大きくなるほど大きな数値を取り、所得格差最大の場合は1.0となる指標となります。ジニ係数という単一の指標で、格差の程度を表現できることになるわけです。