　弾性力学の微分方程式は微小変位問題、つまり変形が目に見えないくらい小さいときに限定された方程式なので、物体が大きく変形したり、特に回転したりするような場合は、上記1項と2項が満たされない可能性があります。CAEソフトのデフォルト設定は微小変形問題となっているので、物体が明らかに回転する場合は、大変形問題として解析する必要があります。

参考文献：

［2］O.C.ツィエンキーヴィッツ｜基礎工学におけるマトリックス有限要素法｜吉識／山田監訳（S50）

メッシュスタディは必要か？

　いくつかの文献では「メッシュスタディ」が必須であると記されています。メッシュスタディとは、要素分割の細かさをいくつか変えてみて、分割の細かさを1段上げても解析結果が変わらないことを確認する作業です。図12の2次要素の例では、Aの時点（分割数5）でメッシュスタディ完了です。1次要素の場合は分割数18でもメッシュスタディが完了したといえません。

　では、通常の業務でメッシュスタディをやっているのでしょうか。400万節点の解析モデルに対してメッシュスタディをやるのでしょうか。節点数が膨大になるのでなかなかできないものです。では、ありがちな例を使って調べてみましょう。

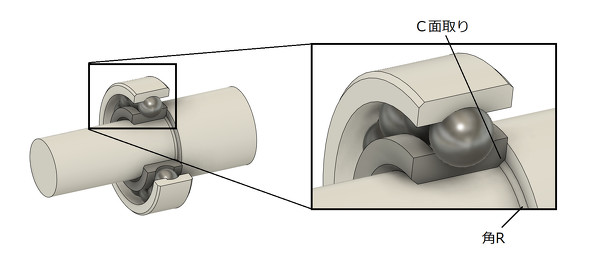
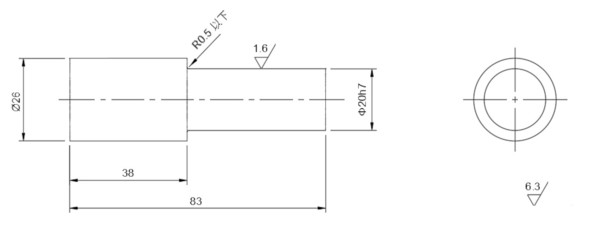
　図14にシャフトとベアリングを示します。ベアリング側にはC面取りがあり、シャフト側の角部には角Rがあります。シャフト側の角RをR0［mm］にすればC面取りは不要になりますが、シャフトは旋盤で製作する（バイトの先端には必ず丸みがあるため）、シャフト側の角Rをゼロにできません。通常は製作図面に「R0.5以下」などの指示をします。シャフトの製作図面は図15のようなイメージでしょうか。

図14　シャフトとベアリング［クリックで拡大］

図15　シャフトの製作図面［クリックで拡大］

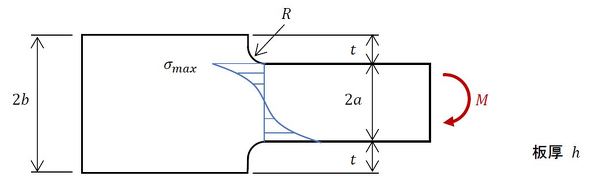
　3次元モデルだと要素数が膨大になるため、図16に示した簡易的な2次元問題（板）に変えます。最大応力は次式で求められます。

式11

図16　角R問題：2次元版［クリックで拡大］

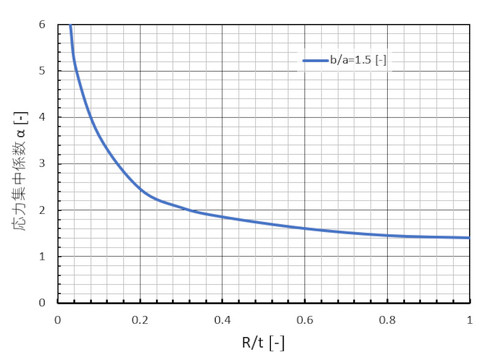
　応力集中係数αは、図17のような感じです。角Rがゼロに近づくと、αが無限大に近づくこともぜひ覚えておいてください。

図17　応力集中係数：段付き板の曲げ（参考文献［1］）［クリックで拡大］

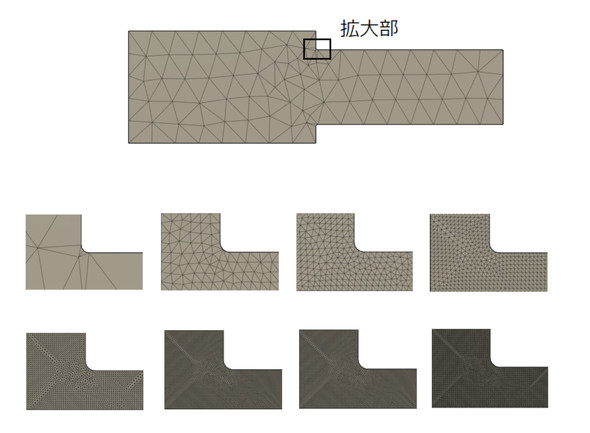
　角Rが小さいほど応力集中係数は大きいので、角Rが0.5［mm］の場合を調べれば、ほとんどの場合に対応できると思います。図18に要素分割図を示します。使った要素は2次要素です。

図18　要素分割図：段付き板の曲げ［クリックで拡大］

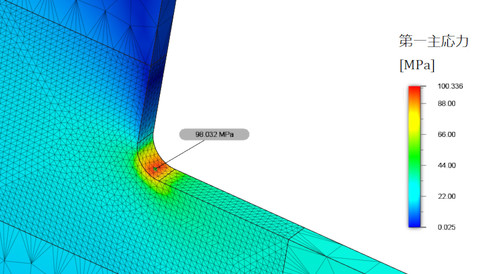
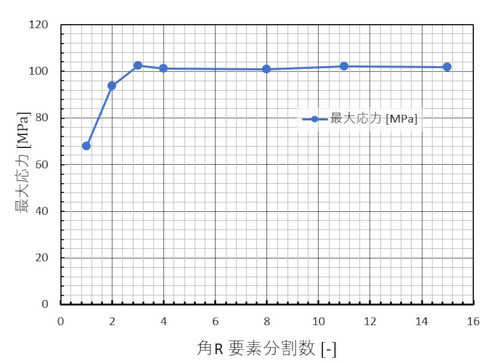
　図19に計算例を、図20に角Rの要素分割数と最大応力の関係を示します。

図19　計算例［クリックで拡大］

図20　角Rの要素分割数と最大応力［クリックで拡大］

　図20の要素分割数2［-］の応力に注目します。最大応力の真値は約100［MPa］だということは推測できるので、要素分割数2［-］の応力は真値の92［％］、誤差8［％］となりました。「2分割、誤差10［％］」は円孔問題で前述しました。つまり、角Rの要素分割数を2［-］とすると、応力は大体10［％］低めに出るということです。

　本連載は、疲労破断の有無の予測をテーマにしていますが、繰り返し荷重部の応力安全率は2.0［-］くらいをとります。この10［％］は安全率に含めて考えてよいかと思います。もし、心配なら安全率を2.2［-］にすればよいことになります。いくつかの文献では安全率が1.2［-］との記載もありますが、このような安全率がとれるのは、「実物大で、かつ実稼働状態の疲労試験を何回も行っている」ときに限られます。読者の方でこのような条件に当てはまるのはまれだと思いますので、安全率は2［-］としました。

　「えっ!?　うちの会社の規定では安全率は8［-］だったはず」と思われた方もいるかもしれませんが、いずれ「昔ながらの安全率」と「最近の安全率」のことも連載の中で触れたいと思います。

　以上のことから、下記条件を満たしていればメッシュスタディは不要と考えています。

（1）2次要素を使っている
（2）角Rでの要素分割数は2［-］以上としている

　「メッシュスタディは1次要素を使っていた過去の遺物」というと少し言い過ぎですかね。角Rが0.5［mm］よりはるかに小さい場合の疲労破壊の有無を予測する方法はいずれ説明します。

四面体要素の形状関数

前のページへ 1|2|3|4 次のページへ