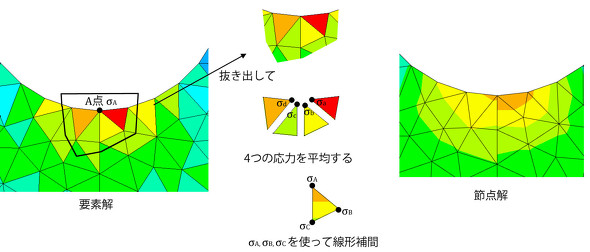
　図5をよく見ると、応力値が隣り合う要素が連続ではありません。図4、図5は「要素解」と呼ばれるもので、これが有限要素法プログラムが計算した値です。しかし、読者の皆さんが見ている応力分布は連続していると思います。普通、設定を変えない限り「節点解」で表示されます。節点解の計算方法を説明します。

　図6左図のA点の節点解σ_Aを要素解から求めます。A点には4つの要素がつながっているので、それらを取り出します。4つの要素は異なる応力値σ_A、σ_b、σ_c、σ_dを持っているのでこれらを平均します。これがA点の節点解σ_Aです。同様の方法で節点解をあと2つ（σ_bと、σ_c）求めます。ここから先はソフトによって違うと思いますが、この例では線形補間しているようです。

図6　節点解の求め方［クリックで拡大］

　何となく、それらしい応力分布になりました。平均化の効果がありましたが、それは見た目が良くなっただけと解釈しています。

解析精度：1次要素と2次要素

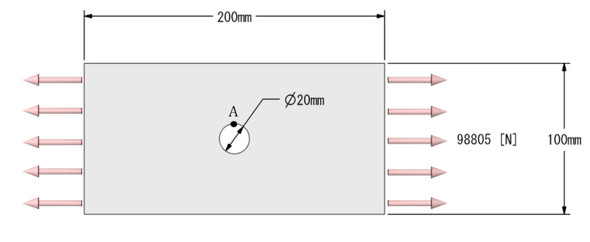
　1次要素と2次要素の解析精度を比較してみましょう。図4のような応力値を使うわけにはいかないので、節点解を使います。図7に計算モチーフを示します。

図7　解析精度の比較のための計算モチーフ［クリックで拡大］

　図7の場合はA点の応力が最大となり、最大応力σ_maxは次式で求まります。

式10

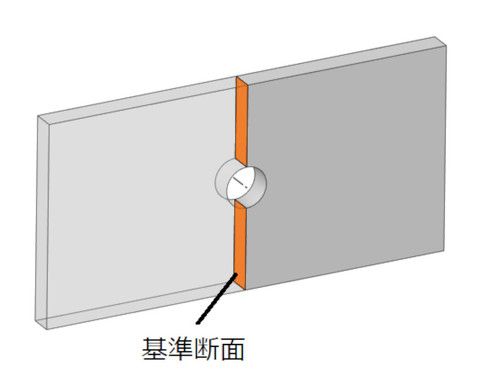
　応力集中係数αは重要な係数です。有限要素法はαの計算が得意です。基準応力は荷重を図8の基準断面の面積で割った値です。「公称応力」といってもいいと思います。いずれ疲労強度の話をするのですが、今後公称応力が多く出てきます。

図8　基準断面［クリックで拡大］

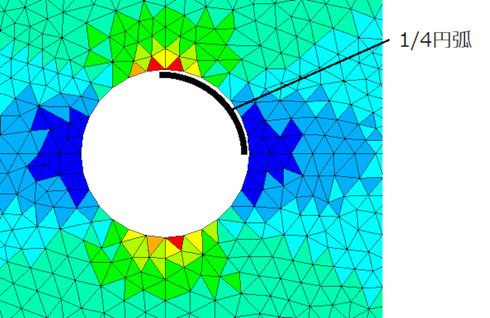
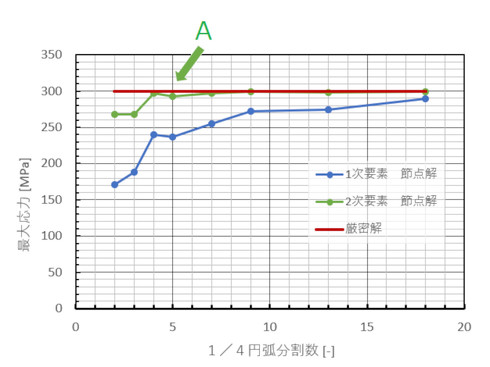
　参考文献［1］によるとαは2.4［-］くらいなので、最大応力は300［MPa］です。板の幅が無限だと応力集中係数は3［-］と求まりますが、この場合は板の幅が有限なので、弾性力学の微分方程式を厳密には解けず、これは何からの方法で求めた近似解と推測されますが、「厳密解」と呼ぶことにします。では、1次要素と2次要素でこの応力が求まるか調べましょう。要素分割の細かさをいろいろと変えて計算しました。図9に要素分割数の定義を示します。要素分割数を1／4（4分の1）円弧上にある要素数とします。

図9　要素分割数の定義［クリックで拡大］

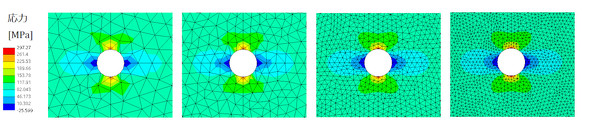
　図10に要素分割をいろいろと変えた解析結果を示します。

図10　要素分割をいろいろ変えた解析結果［クリックで拡大］

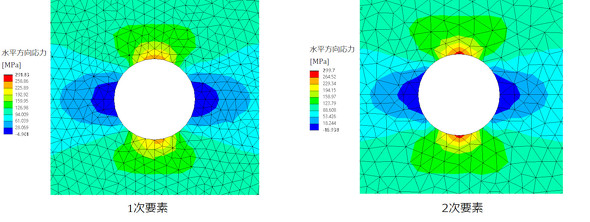
　図11に計算結果の例を、図12に要素分割数と応力値を示します。

図11　計算結果の例［クリックで拡大］

図12　要素分割数と応力値［クリックで拡大］

　図12を見ると、2次要素を使った場合、1／4円弧を4分割しただけでほぼ厳密解となりました。1次要素の場合は18分割でも厳密解になりませんでした。最も分割数の少ない場合の分割数2［-］に注目します。1次要素では半分の応力値しか出ていませんので、この値を使って強度評価するとかなり危険側の判断をしてしまいます。一方、2次要素では厳密解との差は10［％］となりました。「2分割、誤差10［％］」は、後で使うのでしっかりと覚えておいてください。以上のように、1次要素と2次要素では解析精度に大きな違いがあります。

　1次要素と2次要素は「次元が違うくらい」異なることを分かっていただけたでしょうか。この次元の違いは、経済対策の程度の大きさを表す形容詞ではなく、アニメファンがいう「次元の違い」の方に近いです。

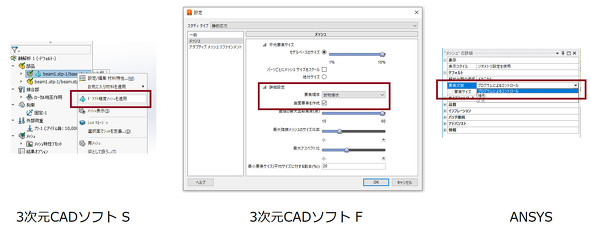
　3D CAD付属のCAEソフトの場合、1次要素と2次要素の選択をするメッセージは特になく、ソフトのデフォルト値に従います。一度デフォルト値を確認していただければと思います。もし1次要素であれば、「今までのオイラの解析、全部そうだったのか……」となります。では、デフォルト設定が1次要素か2次要素かが分かる画面を紹介しておきます。図13です。