シミュレーションによる時刻歴応答解析を理解する：CAEと計測技術を使った振動・騒音対策（13）（4/5 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

対策が必要な箇所の同定

　加工点とステージの相対変位を低減させる案を考えてみましょう。通常は、変形形状を観察すれば対策が必要な位置が分かりますが、今回の例では装置が大きく前後に振れており、前後に振れる振動変位は対象外なので、動画1の変形形状をよ〜く観察してもピンと来るような案は出てきそうにありません。連載第11回で、「相当応力図を表示させると対策が必要なところが分かる」と述べました。相当応力図を示します（動画2）。

動画2　相当応力図

　プレートに大きな応力が発生しているようです。もう少し詳しく見てみます。図7に、時刻0.00838［s］のときの相当応力図を示します。分かりやすいスナップショットが得られました。プレートが変形し、コラムが倒れていることが分かります。

図7　時刻0.00838［s］のときの相当応力図［クリックで拡大］

　図1を見た限りでは、かなりゴツゴツっとした装置で、剛性が高いように思えたのですが、シミュレーションから剛性弱点を見つけることができました。

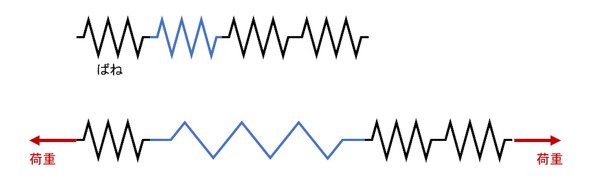
　剛性、つまりばね定数について考察します。ほとんどの機械の剛性は「ばねの直列つなぎである」と考えます。図8上段のようになるでしょうか。1本でもばね定数の小さなばねがあると、それだけ、ビョ〜ンと伸びてしまい、全体のばね定数は最も小さなばね定数で決まります。

図8　ばねの直列つなぎ［クリックで拡大］

　今回の場合、プレートの剛性が全体の剛性を決定付けていたと考えられます。コラムなど、かなりゴツゴツっとした部品もありますが、コラムだけ剛性を上げても効果は期待できません。

対策立案

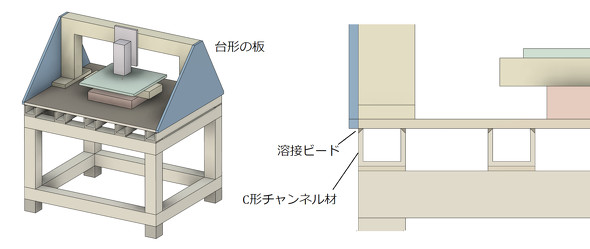
　コラムの倒れを防止するために、側面に台形の板を追加します。さらに、板の剛性を上げるために、プレートの下側にC形チャンネル材を設け、「開先をとった完全溶け込み溶接」でプレートに結合します（図9）。

図9　対策［クリックで拡大］

　動画3に、対策の時刻歴応答解析結果を示します。加工点とステージの相対変位がかなり低減していることが分かります。

動画3　対策の時刻歴応答解析結果

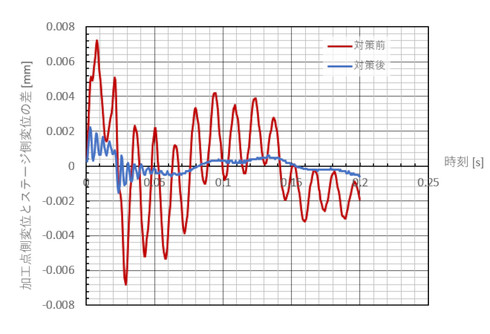
　図10に、対策前後の加工点変位とステージ変位の差を示します。相対変位のpeak-to-peak値が約4分の1になりました。また、対策後の振動周波数が高くなったので振動が早く減衰することも期待できます。

図10　加工点変位とステージ変位の差［クリックで拡大］

　以上が振動時刻応答解析の説明です。