炊飯器のモデリング(その1) 〜おいしいご飯ができるプロセスを科学する〜:1Dモデリングの勘所(22)(2/3 ページ)
お米の構造とお米のモデリング
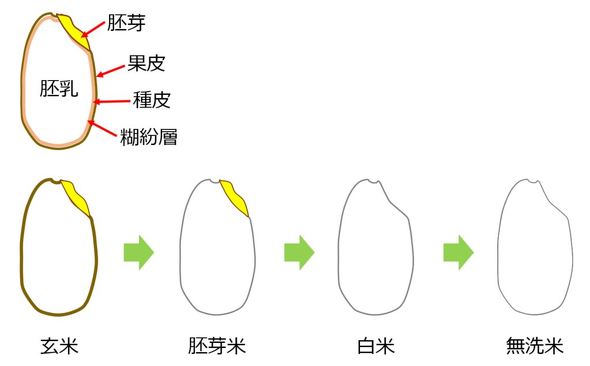
図4左上に玄米の構造を示す。中心にあるのが胚乳でデンプンから構成されていて、この部分が白米になる。胚芽は稲が芽を出す部分で種々の栄養成分が凝縮されている。胚乳の外側には、糊粉(こふん)層、種皮、果皮が構成されている。玄米の状態では食べにくいので、通常は図4下に示すように果皮、種皮を除いた胚芽米、さらに胚芽を取り除いた白米、糊粉層を除去した無洗米が使われている。
図4で示したお米を水と一緒に炊き上げるわけであるが、その前に一定時間、水に浸けて(浸水)、馴染ませておく。お米はもともと一定の割合の水分を含んでおり、浸水、炊飯により、この水分の割合が変化(増加)する。お米に含まれる水分の比率は含水率αとして以下のように定義される(式1)。
ここで、お米単体での含水率をα1、浸水後のお米の含水率をα2、炊飯後のお米の含水率をα3とすると、炊飯プロセスにおける含水率の変化は図5のようになる。最初の段階で質量Aであったお米は、浸水時に水分量Cを、炊飯時に水分量Dを加え、炊飯完了時には質量A+C+Dとなる。水量は最初、Bであったものが、浸水時にC、炊飯時にD、お米に含水され、残ったB−C−D=eが蒸気となって放出される。含水率は、お米の種類(図4下)、銘柄、年度で経験的に最適な値が知られており、この値になるように図5のプロセスを実行することになる。
図5の炊飯プロセスにおけるお米の含水率の変化を式で表現してみる。定義すべき値は以下の通りとする(任意に設定できる)。すなわち、白米1.5合を所定の含水率にするためには、炊飯時間は12分(720s)必要であると仮定し、そのために必要な熱量および熱流束を推定することを目的とする。
- お米の質量:A[kg](白米1合は0.15kgとし、1.5合で0.225kg)
- お米単体の含水率:α1(0.15)
- 浸水後のお米の含水率:α2(0.28)
- 炊飯後のお米の含水率:α3(0.64)
- 加えた水の蒸発率:β(0.05)
- 乾燥米の比熱:Cr[J/kg/K](1600J/kg/K)
- 水の比熱:Cw[J/kg/K](20℃〜100℃の平均値として4199J/kg/K)
- 上昇温度:ΔT[K](20℃→100℃として80K)
- 水の蒸発熱:He[J/kg](2257*103J/kg)
- 炊飯時間:X[s](720s)
一方、求めたい未知数は以下となる。
- お米の乾燥質量:Ad[kg]
- お米の水分質量:Wa[kg]
- 加える水の質量:B[kg]
- 浸水水分質量:C[kg]
- 炊飯水分質量:D[kg]
- 蒸発水分質量:e[kg]
- 炊飯に必要な熱量:E[J]
- 炊飯に必要な平均熱流束:Q[W]
上記の8つの未知数に対して、以下の8つの式が成り立つ。
これらを「Modelica」でテキスト表現すると以下となる。
model riceModeling Real Ad; Real Wa; Real B; Real C; Real D; Real e; Real E; Real Q; parameter Real A=0.225; parameter Real alfa1=0.15; parameter Real alfa2=0.28; parameter Real alfa3=0.64; parameter Real beta=0.05; parameter Real cr=1600; parameter Real cw=4199; parameter Real delT=80; parameter Real He=2257000; parameter Real X=720; equation A=Ad+Wa; B=C+D+e; alfa1=Wa/(Ad+Wa); alfa2=(Wa+C)/(Ad+Wa+C); alfa3=(Wa+C+D)/(Ad+Wa+C+D); beta=e/B; E=(Ad*cr+Wa*cw+B*cw)*delT+e*He; Q=E/X; end riceModeling;
上記の計算を実行すると、
- お米の乾燥質量:Ad=0.191kg
- お米の水分質量:Wa=0.034kg
- 加える水の質量:B=0.322kg
- 浸水水分質量:C=0.041kg
- 炊飯水分質量:D=0.266kg
- 蒸発水分質量:e=0.016kg
- 炊飯に必要な熱量:E=180487J
- 炊飯に必要な平均熱流束:Q=251W
となる。
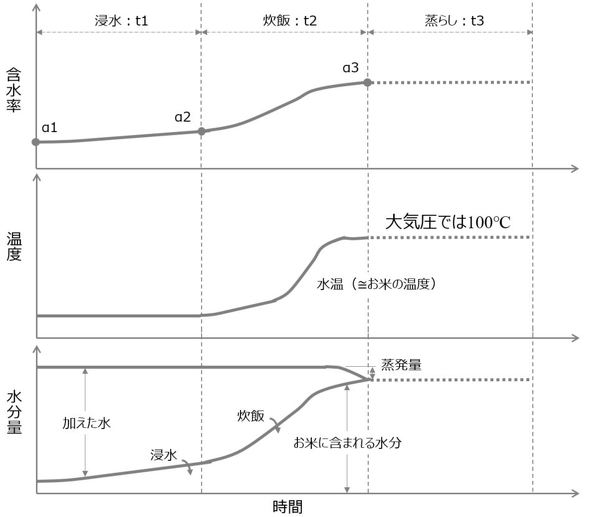
図5のプロセスを横軸に時間をとり、各時間の含水率、温度、水分量の変化を模式的に示したのが図6である。水温と時間を適切にとることにより目標の含水率を実現することになる。前項の「お米をおいしく炊く経験的方法」で述べたように、単に含水率を実現するだけでなく、芯が残らないように均一にむらなく炊き上げるためには、相応の時間と温度変化が必要である。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
 式1
式1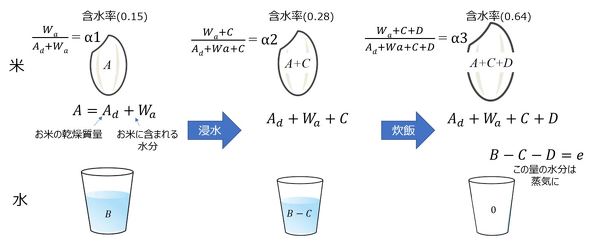
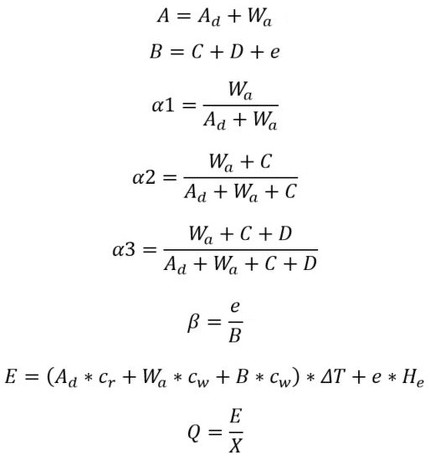 式2〜9 未知数に対する8つの式
式2〜9 未知数に対する8つの式