モデリングツールとしての「Modelica」(その2):1Dモデリングの勘所(14)(2/3 ページ)
テキストベースのモデリングの方法
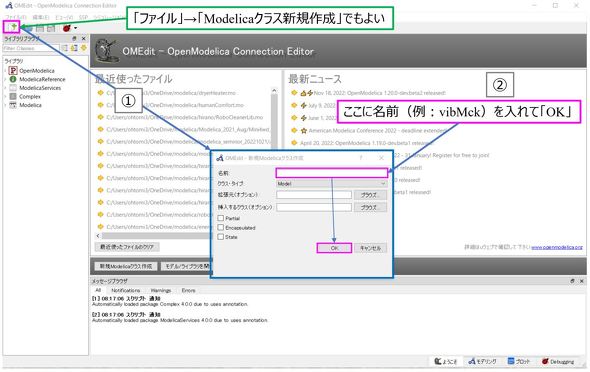
次に、今回の目的である“テキストベースのモデリングの方法”について説明する。まず、GUIエディタ(OMEdit)を立ち上げる。上部アイコンの一番左の[modelicaクラス新規作成]をクリックすると、図5に示すダイアログボックスが表示されるので、新規モデルのクラス名(ここでは「vibMck」とする)を入力する。入力したら[OK]ボタンを押す。
ここで、「クラス」という言葉が出てくるので補足する。Modelicaは、C++などと同様の“オブジェクト指向プログラミング”の考え方を導入している。オブジェクト指向プログラミングでは、全てのモデルはクラスとして定義される。この辺りの仕組みに関しても次回(その3)で説明する。
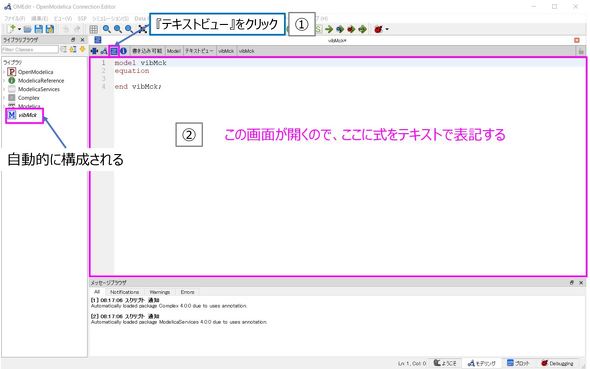
この段階で、左側のライブラリブラウザの「Modelica」の下に「vibMck」が自動的に構成される。この状態で右の画面はダイヤグラムビューになっているので[ダイヤグラムビュー]アイコンの右横の[テキストビュー]アイコンをクリックすると図6のテキストビュー画面が開き、コードが入力できる状態になる。その際、コードの最初の「model vibMck」と、最後の「end vibMck;」の記述は自動生成される。
振動モデルの定式化とモデリング
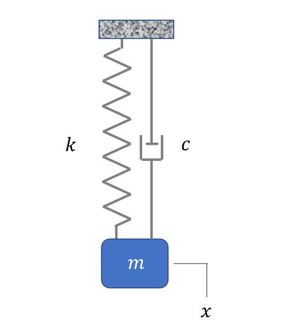
振動モデルとして、図7に示す“1自由度系のマスダンパばねモデル”を考える。
Modelicaでは、もともと微分方程式を記述できる。変数xの微分は、der(x)で記述する。このことを利用して、微分方程式を直接定義して解くことができる。線形の1自由度のマスダンパばねモデルは、以下の微分方程式で表現できる(式1)。
この式は、速度、加速度、力を用いて式2のように表現できる。
従って、この振動モデルのModelicaコードは以下のようになる。
ここでのx、v、aは、それぞれ、マスの位置、速度、加速度である。これらは変数であるので変数宣言する必要がある。ここで扱う変数は実数であるので、実数宣言である「Real」を用いる。変数宣言には、他に整数宣言「Integer」、論理数宣言「Boolean」、文字列宣言「String」がある。いずれも、大文字で始まっている点に注意されたい。ここでは、位置xの初期値を1.0に設定している。変数の初期値を設定するときは、(start=初期値)で定義できる。指定がない場合のデフォルト値は0.0である。
m、c、kは、それぞれ、マスの質量、減衰係数、ばね定数である。これらの値は計算の開始時点で固定されるので「parameter指定」する。parameter指定の他に、固定した変数を扱う「constant指定」、時間離散値を扱う「discrete指定」がある。ここで扱うparameter指定した変数は、シミュレーションの前後で値を変更できる。
equationで始まる部分を「equationセクション」と呼ぶ。equationセクションで、微分方程式を直接定義して解くことができる。前述のように、der(x)は変数xの微分であることを意味する。
ここで、変数と方程式の数が一致している必要がある。この場合、両者の数は4つと一致しているため解くことが可能となる。
コード1のModelicaコードで問題なくシミュレーションは可能であるが、対象となる現象が複雑になってくると、コード中にコメント分を追加したり、単位を明確に表示したりした方が第三者の活用や再利用の際に便利である。そこで、ここでは多少面倒ではあるがコード2のように表記することにする。
単位はSI単位が基本であるので、SI単位に関するライブラリを導入し、これを用いてパラメータ、変数のSI単位の設定を行う。SI単位の表記に関しては、参考文献[1]を参照されたい。また、今回は登場しないが、式表現の際に円周率π、重力加速度gを使用する場合も多い。この場合には、
import Modelica.Constants.pi; import Moderlica.Constants.g_n;
と「import宣言」することにより、pi≡π、g_n≡gと自動的に変換される。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
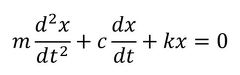 式1
式1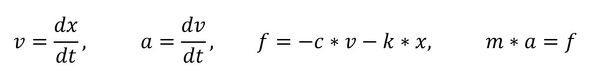 式2
式2 コード1 振動モデルのModelicaコード
コード1 振動モデルのModelicaコード






