トポロジー最適化の実践 〜いろいろな“形の創造”事例〜:フリーFEMソフトとExcelマクロで形状最適化(8)(4/7 ページ)
形状の創造
次に、有限要素法の境界条件だけを与えて、どのような形状になるかを見てみましょう。
図19のようなLISAのデータを作ってください。領域のサイズは、1.6[m]×1.0[m]、厚さは0.1[m]です。a=0.2[-]として、与えられた領域の体積の0.2倍の物体になることを目標としましょう。Excelファイルを図20に示します。
図21に計算結果を示します。アーチ橋ができました。生まれて一度もアーチ橋を見たことのない人がこの形状を考案するのに要する時間を想像すると、今回の方法は「形の創造」に有効な手段だと思います。
図22にf(ρ1、ρ2、ρ3……ρne)の変化を示します。物体に蓄えられる仕事量(エネルギー)が最小化されていることが分かります。
今回の最適化問題の最終形状を図23に示します。自動車レースのチェッカーフラグというか、白と黒の市松模様が出ています。図23のA部については人間が結果をかみ砕いて、図23右図のように橋桁を細いワイヤでつるせばよいとの発想が出てきます。しかし、少し無理がありますね……。
図24に、骨の断面図を示します。軽石というかスポンジのようですね。チェッカーフラグはこのスポンジ構造を示唆しているのではないかと解釈しています。生物の場当たり的な進化と最適化のアルゴリズムの結果が一致したのでしょうか。3Dプリンタの出現でラティス構造の部品を作ることができるようになりました。チェッカーフラグはラティス構造にすればよいとの発想もあると思います。
しかし、20年以上も前のことですが、トポロジー最適化の研究は「チェッカーフラグ・グレー領域・小骨は悪」として進化していきます。これについては、連載第9回以降でお話します。
もう1つ、形の創造事例を紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

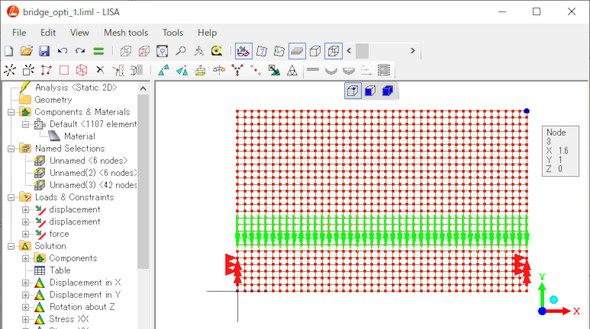
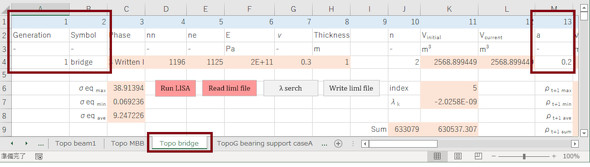

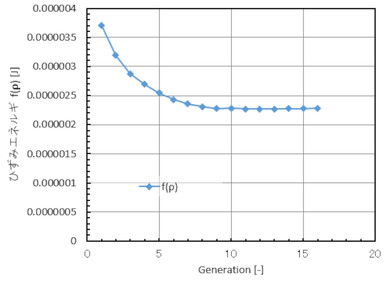
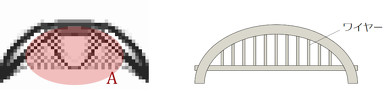
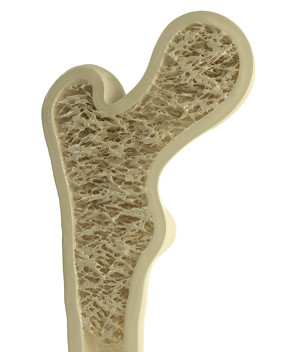 図24 骨の断面(arinarici/iStock)
図24 骨の断面(arinarici/iStock)





