　「戻り回転による緩み」は、軸力がゼロになるまで回転が進行するので、どれだけマージンをとっても安全な設計とはなりません。回転を止める必要があります。「戻り回転によらない緩み」は、理想的な締結ができたとしても10～20［％］の軸力低下があります。この軸力低下を考慮したマージンを取ることになります。このために、設計段階でボルトが本来発揮する軸力よりも小さな軸力が発生するとして、CAE解析をします。つまり、前項ではボルト軸力を7318［N］として解析しましたが、これが“2分の1になってしまった”と考えて、ボルト穴稜線への外力を3659［N］として解析し、拘束したボルト穴稜線の反力がプラスになるかどうかを調べます。反力がプラスであれば、マージン、つまり安全率は2以上あると判断します。

　この方法で安全率を数値化することにより、ボルト径とボルト本数の決定を“経験と勘”ではなく、論理的に決めることができます。なお、ボルトの緩みについては、以降の連載で詳しく解説します。

よくある普通の荷重が作用する場合（その2）

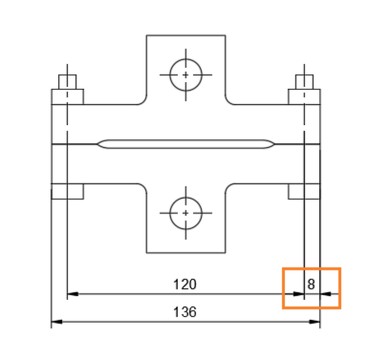
　図12に示したように、被締結体がてこのように振る舞い、荷重Wと比較してはるかに大きな力Bがボルトに作用するので、図11の15［mm］という寸法を8［mm］まで小さくして検討します。図21に寸法を示します。

図21　検討対象【2】［クリックで拡大］

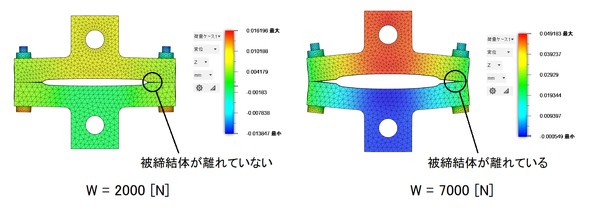
　図13に示した境界条件で、接触要素を用いた解析結果を図22に示します。左側はW＝2000［N］の場合で、被締結体のボルト穴部で被締結体同士は離れていません。右側はW＝7000［N］の場合で、被締結体同士は離れています。

図22　接触要素を用いた解析結果：Tフランジ［クリックで拡大］

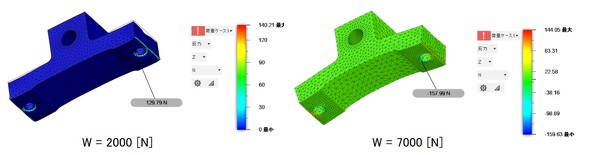
　では、設計者CAEモデルで解析します。解析結果を図23に示します。W＝2000［N］の場合、ボルト穴稜線の反力の最小値は129.79［N］とプラス値となり、被締結体が離れないことになります。W＝7000［N］の場合、反力の最小値は－157.99［N］となり、被締結体が離れていることになります。

図23　設計者CAE解析モデルによる解析結果［クリックで拡大］

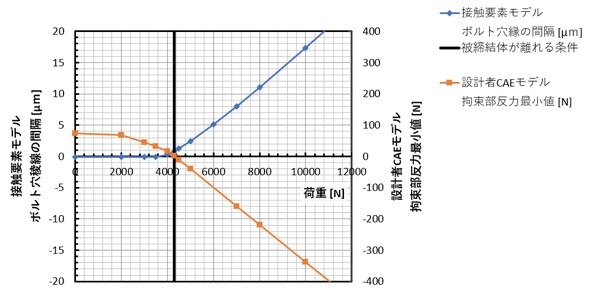
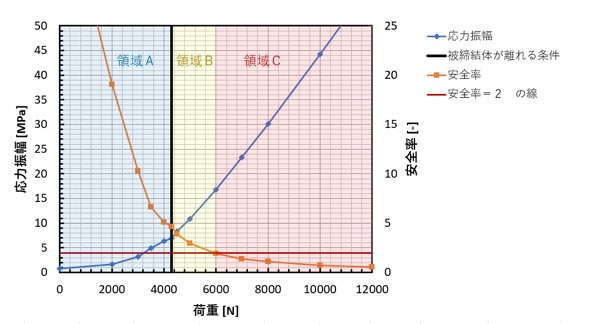
　接触要素を用いたモデルで求めたボルト穴稜線の間隔と、設計者CAEモデルで求めた拘束部反力の最小値を図24に示します。青色の線はボルト穴稜線の間隔で、オレンジ色の線は拘束部反力の最小値で、図24中央の黒色の線は設計者CAEモデルで拘束した稜線の反力の最小値がちょうどゼロになる荷重です。この荷重は4295［N］と、前項の5538［N］からかなり小さくなりました。ボルト穴の中心からエッジまでの距離も重要な設計パラメータです。

図24　荷重を変化させたときの被締結体の間隔と拘束部反力最小値［クリックで拡大］

　接触要素を使ったモデルを用いて求めた、荷重Wを変化させたときのボルトの応力振幅と安全率を図25に示します。図25中央の黒色の線は、設計者CAEモデルで拘束した稜線の反力の最小値がちょうどゼロになる荷重です。このときの安全率は4.68［-］です。黒色の線を境に、応力振幅と安全率が急上昇しています。