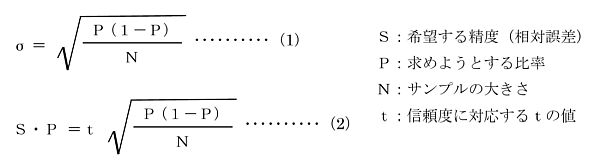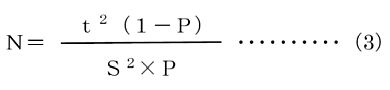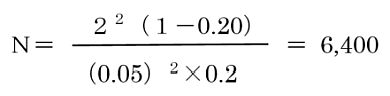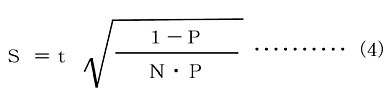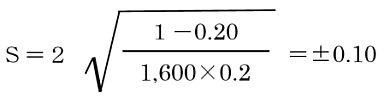「ワーク・サンプリング法」は作業管理の問題解決に最適：よくわかる「標準時間」のはなし（9）（3/4 ページ）

[福田 祐二／MIC綜合事務所所長，MONOist]

5．ワーク・サンプリング法の基礎となる統計理論

　ワーク・サンプリング法は、確率の法則に基礎を置くものです。大きなグループからランダムに採ったサンプルは、元のグループと似た性格を持っています。もし、サンプルの数が十分に大きければ、サンプルの性格は元のグループ、すなわち母集団の性質とほぼ一致します。ただし、ランダムに抜き取ったサンプルであることが必須の要件です。

5.1 正規分布

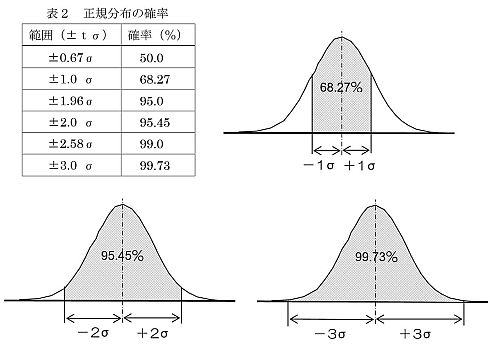
　正規分布は、両側に標準偏差σのある倍率をとった部分の曲線下の面積が重要となります。±2σの領域では95.45％が入ります。ワーク・サンプリング法での信頼度は95％を用いますが、正規分布曲線の±2σの領域は95.45％ですから、信頼度95％を満足させる実測値は±2σの域にあるということがいえます。信頼度95％における誤差範囲は2倍の標準偏差となり、これが絶対誤差といわれるものです。

　絶対誤差が求めようとする比率Pに対して、どれだけの割合に相当するかを示すのに相対誤差Sが用いられます。すなわち、“絶対誤差＝相対誤差S×求めようとする比率P”の関係となります。

　相対誤差と絶対誤差の関係を物差しを例に考えてみます。物差しの長さの正確さを示すのに「この物差しの誤差は、±acmである」と、「この物差しの精度は±b％である」の2通りが考えられます。物差しの長さをLとすれば、“b＝a／L×100”となります。

　「この物差しの誤差は、±acmである」は、±acmの誤差というだけで、正確さの表し方としては不完全です。この場合は必ず、全長Lを示す必要があります。これに反して「この物差しの精度は±b％である」のような場合は、全長を示さなくても正確さの程度は分かります。±acmを絶対誤差、±b％を相対誤差（または精度）といいます。

　ワーク・サンプリング法においても2つの誤差が考えられます。観測回数を無限に多くすれば求めようとする比率Pは正確になりますが、比率の用途によっては、それほどの正確さを必要としない場合もあります。この許容された誤差を相対誤差と絶対誤差で表すと、“絶対誤差＝相対誤差S×求めようとする比率P”となります。

表2　正規分布の確率と標準偏差σの関係（クリックで拡大）

5.2 信頼度

　ワーク・サンプリング法におけるσは、以下の式（1）であると考えられますので、式（2）としてもよいことが分かります。正規分布の確率をそのまま信頼度としてtを求め、式（2）でNを計算することができます。

　例えば、信頼度95％として、母集団の比率20％を精度±5％で求めるためのサンプルの大きさ（観測数）を求める場合、以下のように算出します。

　信頼度95％に対応するtは先ほど示した表2から、t＝1.96≒2となります。また、P＝20％＝0.20、S＝±5％＝±0.05です。これらの値を、式（2）を変形した式（3）へ代入して計算すると、サンプルの大きさ（N）＝6400という値が求まります。

式（2）を変形すると

となり、

式（3）に代入すると

という結果が得られます。

　また、サンプルの大きさが1600で20％という観測結果が得られたとします。信頼度を95％として母集団の比率をどの程度に見たらいいがという設問については、以下の算出式で求めることができます。

　その結果、母集団の比率は……

20％±（20×0.1）％＝（20±2）％

となり、18％〜22％であると見ることができます。

　式（2）を変形すると、

となり、

　式（4）に代入すれば

となります。