寸法測定をする前に確認したい基本的なこと：寸法を実感する！ 測定講座（7）（2/3 ページ）

[木下悟志／プラーナー，MONOist]

量産性の確認

　量産フェーズに近くなると、「量産性の確認」ということが大変重要になります。その場合に、必要なサンプル数はどう考えるでしょうか。一般的には30個は必要であると聞いたことありませんか？　その数の根拠について考えてみましょう。

　その根拠は、「工程能力指数」というものに基づくと考えられます。ここでは、工程能力指数（Cp、Cpk）についての詳しい説明は割愛しますが、この指数は、製品に許容される規格値の幅と製品のばらつきとの関係を比率で検証するもので、量産性の判定に関して非常に有効な方法です。また厳しい品質保証を求める業界では定常的に確認されている手法です。その大前提となっているのが、製品の真値（品物の真値のばらつきと、測定値のばらつきを含む）が正規分布していることなのです。

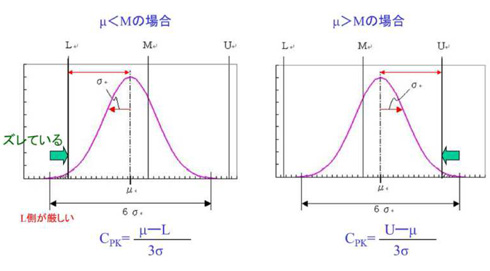
　図1はCpkと呼ばれる平均値（μ）の片寄りを考慮して、許容規格値（L〜U）とばらつき（σ）との検証をするものです。そのためには、正確にばらつきσを求める必要があります。

図1：Cpkと正規分布との関係

　そこで、一般的には、量産と同様の工程を用いて試作品を複数作って決められた特性と公差値に対して測定し、この指数を求め、この比率が大きくなるようにします。つまり、規格幅に対してばらつきの値が十分小さくなることを確認してから量産に入ることで、市場不良の発生確率をゼロにして、また量産での不良率の極小化の検証をするのです。そのサンプル数が、一般的には30個と言われます。それは、正規分布における標準偏差（s、あるいはσ）を求める式を検証してみると分かります。

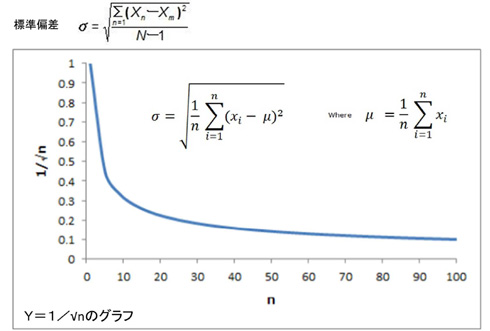
　標準偏差を求める式は以下のようになります。

図2：Y＝1/√nのグラフ

　各測定値と平均値の差の2乗の総和を測定回数で除した値の平方根ですが、ここで、図2のY＝1／√nのグラフを眺めてみると、x＝30近くで傾斜がなだらかになって、落ち着くのが分かります。つまり、これ以上サンプル数を増やす意味がないといえるのです。