MRJはいかにして設計されたのか:CAE最前線―MRJ事例に見る航空機設計でのシミュレーション活用(3/4 ページ)
神経回路網を模擬して結果を可視化する
このようにしてパレート最適解を求めることはできたが、目的関数が増えるにつれて、解集合を読み解くのは大変になる。図7のように、目的関数が2つであれば2次元のグラフ、3つであれば3次元のグラフで表せるが、4つ以上になると可視化、つまり解の分布の直感的な把握ができなくなってしまうからだ。そこで大林氏らが適用した新たな技術が、データマイニング手法の1つである自己組織化マップ(SOM:self-organizing map)である。
SOMは脳の神経細胞同士のつながりをコンピュータ上で再現したモデルだ。脳の神経細胞を考える際に重要なのは、各細胞の位置や細胞間の距離ではなく、それぞれのつながり方である。このモデルを応用して解を細胞に対応させ、各解の座標や距離の関係をなくして、いかに解同士が似ているかのみに着目して並べ、2次元のマップに落とし込むという。つまり多次元の情報を2次元で表現することができるようになる(図8)。
例えばMRJの概念設計で行われた「エンジンを付けた一般的な翼形態の多目的最適化」(流体および構造の連成解析)では、目的関数を3つ設定した。すなわち
- 抵抗値の最小化(図9)
- 主翼の根元上部に生じる圧力変化の最小化(図10)
- 機体重量の最小化
である。
なお主翼の根元に生じる圧力を最小化するのは衝撃波が生じるのを防ぐためである。この場所の圧力変動が大きいと衝撃波が発生し、また機体の抵抗も大きくなってしまうからだ。これらの目的関数に対して、26個の設計変数で最適化を行った後に、とくに性能に影響する設計変数をあらためて10個選び出してデータマイニングを行った。具体的に設計変数は、翼断面が最大厚みとなる位置およびその厚さ、翼下面が最大厚みとなる位置およびその厚さ、そして前桁(主翼の中に翼幅方向に渡される骨部材)の高さの5変数、それをエンジン側と胴体側の2断面について、合計10個である(図11、図12)。
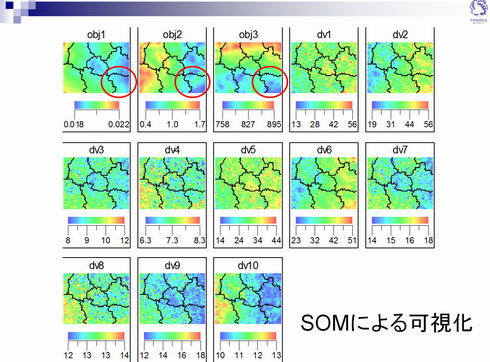
図13のobj1〜3が最適化の結果から作成した目的関数1〜3のSOMである。目的関数の値の大小を赤〜青のカラーで表している。これらを見ると、マップの右下の領域は3枚全てで青いことが分かる。これが「設計空間におけるスイートスポット」となる。また図13のdv1〜10は設計変数10個それぞれの値の大小をカラーで表したものだ。スイートスポットとなる右下の領域に注目してみると、例えば設計変数6(エンジン側の最大厚みの位置)は上げればよいと分かる。つまり最大厚みを持つ位置をなるべく後ろに持っていけば目的関数が小さくなるということだ。このような機能の可視化は設計の現場において大きな効果を発揮しているという。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
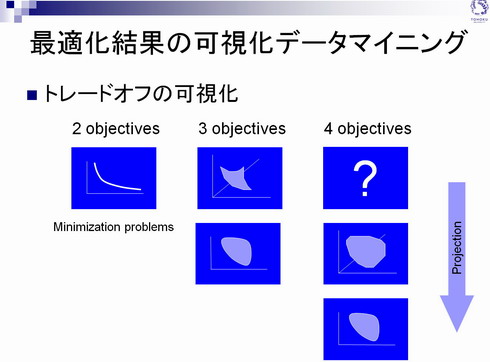
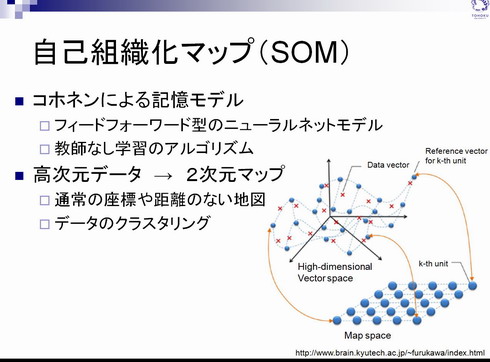

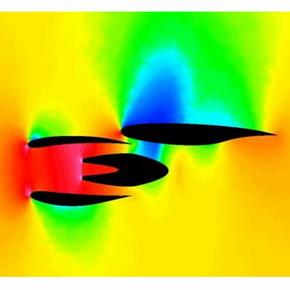 図9(左)航空機の機体表面の圧力分布と、 図10(右)における主翼およびエンジン部分(η=0.29)の断面における圧力分布。右上の主翼上部にある青い部分の圧力変化を抑えることが必要
図9(左)航空機の機体表面の圧力分布と、 図10(右)における主翼およびエンジン部分(η=0.29)の断面における圧力分布。右上の主翼上部にある青い部分の圧力変化を抑えることが必要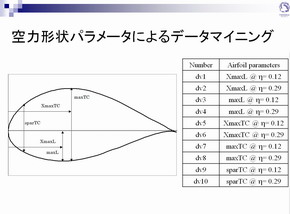
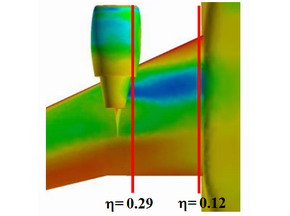 図11(左)主翼2断面の設計変数を10個選び出し、最適な翼形状の探索を行った。図12(右)主翼の根元近く(η=0.12)とエンジン近く(η=0.29)の2断面
図11(左)主翼2断面の設計変数を10個選び出し、最適な翼形状の探索を行った。図12(右)主翼の根元近く(η=0.12)とエンジン近く(η=0.29)の2断面