複数次元の公差積み上げはとても疲れるよ:公差解析 実践の基本(1)(4/4 ページ)
ノン! ノンノーンッ!! ユー、ここで赤字でチェックしたのは、何に関係する寸法ナノ?
このピンが付いた部品のピンと、ボックスの穴に関係する寸法だよ……。だってぶつかってるんでしょ……。
ぶつかるのは確かに「ピンとボックスの位置のズレ」によって生じる現象ダネ。デモー、もうちょっとだけ問題を理解してからチェックした方がいいんじゃないカナ?
もう疲れたよ、おじさん……。
ヘイッ! 頑張るノYO。この風あげるから!! ブーン!
おじさんは頭の帽子の扇風機の風をアズーに向け、励ますのでした。ついでに、ホノさんの多くない頭髪もそよいでいます。
何とか復活ぅ〜。ホノさんの毛は和むなぁ……。
んー?
よしよし……。じゃあみんなでやりましょ。まず「ぶつかる」ってのはさっきおじさんが言ったように位置ピンと穴の位置がズレているから起こっているのよね。ということは、「あんなとき」や「こんなとき」に起こるわけね(図11)。
ぶつかる場所もそれぞれだな。
ということは、関連する寸法もちょっと違ってくるんじゃないかな? 例えばX軸とY軸、みたいなのぅ。
そうだね。じゃあもう一度……。寸法の横にX、Yって書いてそれぞれ関係するところにチェックを付けていくね(図12)。
寸法にもそれぞれ成分があるんだから、計算の結果にも成分がないと、どの寸法を足したらいいのかよく分からなくなっちゃうね……。
イエス! 手計算するなら、方向は決めておいた方が楽なのネ〜。
本当だのぅ。気付かないと、おかしな結果が出てきてしまうねぇ。
ちょっとここら辺で一息入れない?
お、そうだね。ガリクソン君ならうちの売店にも売っているから、みんなで買いにいこうかねぇ。
さんせーい! 大賛成! ガリクソン君を食べてから係数は計算することにしよう!
この夏のガリクソン君パワーは計り知れないな……。
「おじさんも一緒にどお?」と、アズーが振り返ると、「ガリクソン君」を名乗ったおじさんの姿はありませんでした。
ここまでのおさらい
さて、今回はより現実に近い公差解析をお届けするべく、サブラック風の部品を使ったお題を作りました。これまでは1次元、2次元+αの公差積み上げの問題でしたが、今回は3次元の空間内に関連する寸法がちりばめられています。
ホノさんは「こいつはぶつかっているなぁ……」と言っていますが、これは「ボックスの穴とピン付き部品のピンが干渉している」ということになります。干渉にも方向があり、公差解析を行う場合も、その方向に対して積み上げる寸法が変わってきます。
今回、アズーたちはX方向とY方向という2成分で計算をすることにしました。皆さんも図13のようなケースで「こういう成分は?」という疑問があるかもしれません。
まずはX成分とY成分の合成成分として考えてみましょう(正確には実際の公差域とは少し違いがあります)。それでも特定の成分での干渉が見受けられる場合は(係数の算出が大変になってしまいますが)、ロックオンして計算するのもいいでしょう。
次回は係数を出して、次のステップに進んでいきます。3次元の公差解析は大変ですが、頑張りましょう!(次回へ続く)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
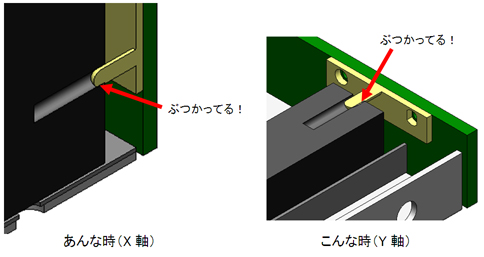 図11 ぶつかってる!
図11 ぶつかってる!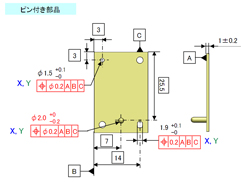
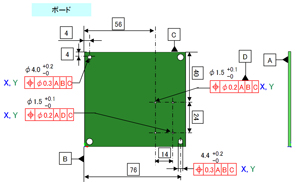
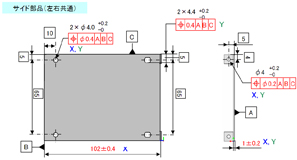
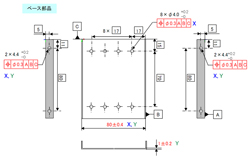
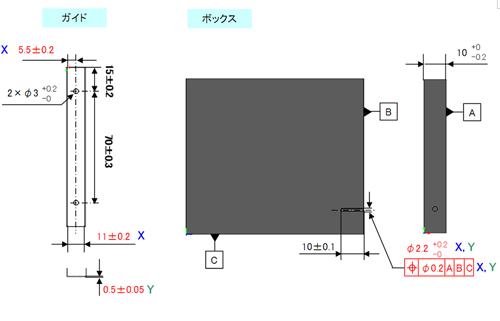
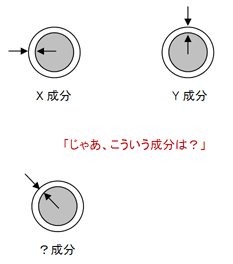 図13 こういう成分は?
図13 こういう成分は?






