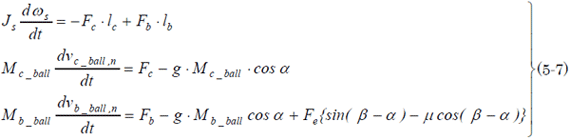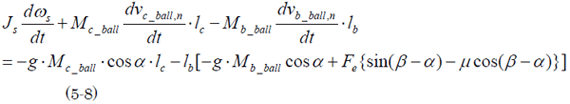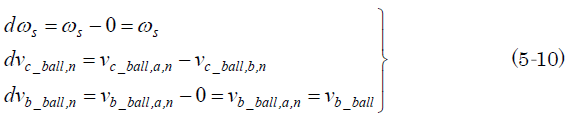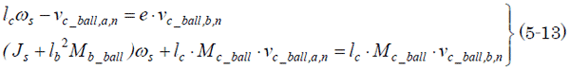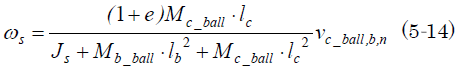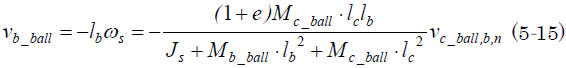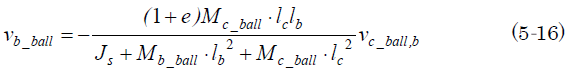ボールがスコーンと跳ねる高さを調整せよ:ピタゴラスイッチの計算書を作ろう(5)(2/4 ページ)
エネルギーの保存
草太「シーソーの上に置かれたバスケットボールが、台車から落ちてきたボールによって、てこの原理で跳ね上げられるときの高さはどうやって計算するのかな? 」
編集部より、読者の皆さまへ
以降で出てくる数式をメモ帳やノートなどに書き取るなどして、実際に計算しながら読み進めてみてください。より理解が深まります。
草太「まず、バスケットボールの質量を『Mb_ball』、シーソー板から跳ね上がるときの速度を『vb_ball』、跳ね上がりの最大高さを『hb_max』とすれば、重力加速度を『g』として、エネルギー保存の式から、以下のような式になる」
草太「だからバスケットボールが跳ね上がる高さhb_maxは、こう」
*変数については前ページの図5.1を参照してください
草太「跳ね上がりの最大高さhb_max=200mmとして、バスケットボールが跳ね上がるときの速度を計算すると……」
草太「でも変だね。跳ね上がり高さはバスケットボールの質量に関係しないよ」
銀二「いまごろ何をいっているんだね。ガリレオのピサの斜塔の実験の故事を知らないのか?」
草太「『ピサの斜塔から質量の違う2つの物体を落としたら同時に着地した』ってやつでしょ。この実験から重力による落下速度はその物体の質量の大きさによらないってことを見つけたんだよね。そうか。この場合はその反対ってことになるんだ」
銀二「結局、バスケットボールの跳ね上がり高さはシーソー板から飛び跳ねるときの速度で決まる」
草太「シーソー板から飛び跳ねるときの速度がバスケットボールの質量で違ってくるってことだね。ではその速度はなんで決まるかといえば、台車から落ちてきたボールがシーソー板と衝突して、その衝突によって回転するシーソー板の回転角速度だ。そこで、台車から落ちてきたボールがシーソー板とどのくらいの速度で衝突し、その衝突によってシーソー板がどのくらいの角速度で回転し、シーソー板の反対側のバスケットボールをどのくらいの速度で跳ね上げるかって問題になるわけだね」
銀二「だいたいそんなとこだね。問題を解くとき、具体的な計算に入る前にいまのような手順を考える必要があるんだ。シーソー板から飛び跳ねるときのバスケットボールの速度を計算してみるのもいいけど、跳ね上がり速度が分かれば、(5-2)から跳ね上がる高さも分かるから、バスケットボールの質量をパラメータとして、跳ね上がり高さを求めてみようか」
草太は、いままで学習してきたエネルギーの保存の法則、反発係数の定義式、運動量保存の法則を思い出し、ノートに式を書き込みながら叔父さんに説明をしました。
草太のノート
台車から落下するときの台車のボールの高さhc_ballと、落下するときの速度vc_ballおよびそのボールがシーソー板と衝突する直前の速度vc_ballとbとの間には、エネルギーの保存式が成り立つから、台車の中のボールの質量をMc_ballとして、
右辺の添え字「b」は衝突前の「before」を意味していることは前回と同じだからいいよね。前回同様、ボールの回転エネルギーは無視するよ。(5-4)から台車の中のボールがシーソー板と衝突する直前の速度vc_ball,、bは、
で計算できる。
速度の符号は下向きが負、上向きが正だよ。だから(5-5)にはマイナス符号が付いている。
そしてシーソー板が台車のボールとの衝突によって角速度ωsで回転すると、シーソー回転支点と衝突点までの回転の腕の長さをlcとすれば、シーソー板の衝突点速度はlcωsだから、反発係数を「e」として、衝突の定義式から、
と書ける(記号は図5.2参照)。
(5-6)によって、衝突前後の台車のボールの速度とシーソー板の回転角速度ωsを関係付けることができる。添え字「a」は衝突後の「after」を、「n」はシーソー板の方法線方向を意味しているよ(図5.2参照。シーソー板の回転角速度ωsは反時計周りを正としていることに注意!)。
一方、シーソー板のオイラーの運動方程式と、各ボールとシーソー板法線方向のニュートンの運動方程式はそれぞれ、以下のように書ける。
もちろんωs、Jsはシーソー板の回転角速度と慣性モーメントだ(図5.2)。
そしてFc、Fbは台車からのボールがシーソー板と衝突したときに発生する衝撃力だ。ただしFeはバスケットボールが受け板から受ける力で衝撃力ではないよ。「μ」はバスケットボールと受け板との間の摩擦係数だ。
(5-7)において、衝撃力Fc、Fbはを消去すると
となる。
(5-8)に衝突時間dtを掛けると、dtは非常に短いから
となって、衝突前後の速度差を
と書けば、(5-9)は
だ。
台車のボールがシーソー板と衝突した後のバスケットボールの飛び跳ね速度 は、シーソー板の角速度ωsを使えば、こうだ。
ここで右辺に負符号が付いているのは、シーソー板の回転は反時計周りを正としているからだよ。
よって(5-6) と(5-11)は、(5-12)を使ってvc_ball、a、nとωsについての次の連立方程式を構成することになる。
これをωsについて解くと
だ。従ってバスケットボールの飛び跳ね速度vb_ballは
となる。
右辺の台車のボールの衝突速度vc_ball、b、nは下向きの速度だから負だね。だからバスケットボールの飛び跳ね速度vb_ballは上向きの正の値となる。
ここで、台車のボールがシーソー板と衝突する前の法線速度vc_ball、b、nは直線スロープ2からのボールの落下軌跡を計算しないと正確な値は分からない。しかし、接線方向の速度は小さいと仮定すれば、(5-5)の衝突速度vc_ball、bにほぼ等しいと考えられるから(5-15)は
と書ける。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
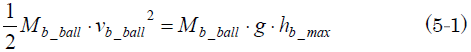
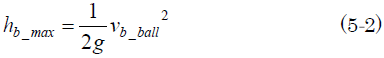
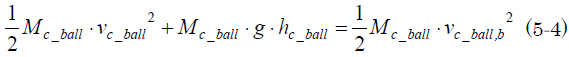
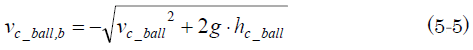
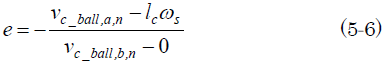
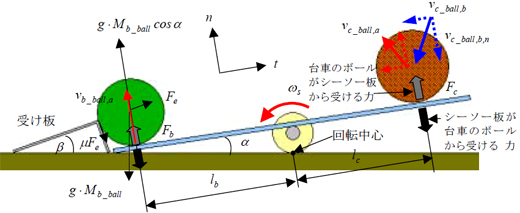 図5.2 草太が作ったシーソーの構想図
図5.2 草太が作ったシーソーの構想図