直交配列実験を基にした重回帰分析の実務:Excelで学ぶ実験計画法の基礎(4)(4/5 ページ)
総まとめ
これまでさまざまな方法を紹介してきましたが、ここからは、データ解析の総復習をしていきます。少々手間は掛かりますが、図15〜17に掲載した各データをお手持ちのExcelに入力していただき、検定も含めてデータを解析してみてください。
データ1の解析
まずは、データの要約です。バラツキのあるデータを眺めていても結論は出ませんので、統計の常とう手段、データの要約を実施します。要約といっても難しいことはありません、皆さんがご存じの平均値を計算するのが基本です。
平均値を見ると、差があることが分かりますが、すべてのデータが平均値と同じ値になっているわけではありません。バラツキの状態によって、この差の相対的な意味合いは異なってきます。そこでバラツキの大きさを示す標準偏差を計算します(図18)。
数値は計算を間違えない限り正確です。ただし、情報伝達といった視点から見ると、必ずしも優れものともはいえません。その理由は、数値では頭の中でイメージをつかみにくいからです。そこでグラフを利用して状況の視覚化を試みます。留意点は、平均値だけでなく、バラツキを示す標準偏差もエラーバーを使い表現することです。グラフを見るとバラツキ以上の差が見受けられます(図19)。水準間には意味のある差があるといえそうです。そして、バラツキには違いのないことが分かります。
ここで結論付けをしてもよいのですが、この結果は、あくまでも数少ない実験のデータから導かれた結論です。この結果に普遍性があり、一般化できるのか、すなわち母平均に差があるといえるのか、実証するための方法が統計的仮説検定でした。特性値に影響する要因として1つの因子を実験に取り上げられています。このように1つの因子を対象に実施する実験は一元配置実験と呼ばれ、対応する統計的仮説検定の方法は一元配置分散分析でした。一元配置分散分析はExcelの分析ツールで実行が可能です(図20)。
分散分析を実行すると、さまざまな数値が出力されますが、実用的に見るべき数値は1個所だけ、P−値(一般のp値、有意水準に相当)の下にある数値です。P−値が0.05を下回る場合、因子の効果は統計的に有意で、水準間の母平均に差があるといえます。水準Aの平均値はほかの水準より高いといえそうです。
「いえそうです」といった表現を用いたのは、先の連載では説明しませんでしたが、多重検定と呼ばれる方法を用いて、さらに水準間の比較を実施して初めていえるからなのですが、話がややこしくなりますので、多重検定とは何かをお知りになりたい方は別途統計の専門書をご参照ください。ただし、水準が2つの場合は、分散分析の結果をもって、水準間の母平均に差があると主張できます。
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- AIエージェントが代わりに働くようになったら人は何をするの?
- 永守氏がニデック完全退任、「経営者としての私の物語にピリオド」
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク
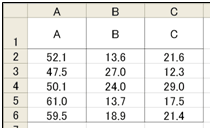 図15 データ1 感光剤
図15 データ1 感光剤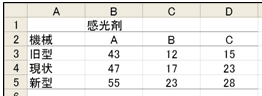 図16 データ2 感光剤と機械
図16 データ2 感光剤と機械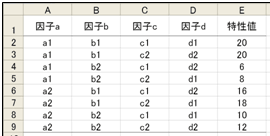 図17 データ3 4つの因子を組合せた試作品
図17 データ3 4つの因子を組合せた試作品 図18 データ1の平均値と標準偏差
図18 データ1の平均値と標準偏差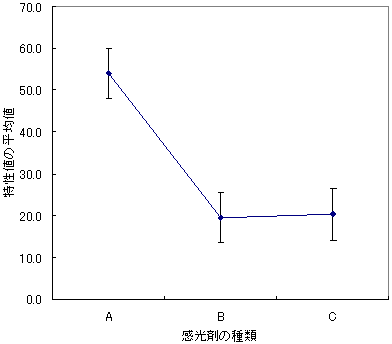 図19 データ1の視覚化による検討
図19 データ1の視覚化による検討