推測統計の基礎―― 一元/二元配置分散分析:Excelで学ぶ実験計画法の基礎(2)(4/5 ページ)
Excelで一元配置分散分析を行う(Excelのバージョンは2003)
I 検定法の選択
今回の例は因子の数が1つ、特に外れ値もないため、一元配置分散分析を選択します。
手順1
Excelでは、仕様の都合上、列を水準に取りデータを入力します。今回の例では図8のようにデータを準備します。
手順2
メニューから[ツール]→[分析ツール]→[分散分析:一元配置]を選択します。
手順3
表示されるダイアログにデータ範囲などを指定します。図8のようにデータを入力した場合の、ダイアログの指定は図10のとおりです。出力オプションは、お好みに合わせて変更してください。
[OK]を押すと、計算結果が出力されます。
II 判定
[P-値]の下のセルの値がP値で0.0453となっています。有意水準を0.05とすると、P値は0.05以下なので、「水準5%で、製品重量の平均値の差は有意である」といえます。今回実施した抜き取り検査の標本だけに限らず、昼勤と夜勤の製品重量の平均値には差があるといえます。
二元配置実験
【STEP 0】データセットの準備
ここで、この製品を製造する機械に着目してみます。これらの機械はメンテナンスのため、仕様は同じ型番が異なる3つの機械(A=1、B=2、C=3)を4時間サイクルで交代させていました。機械の違いも製品重量に影響している可能性があります。そこで、機械を1つの因子と見なし解析に投入してみます。データセットは図12のとおりです。
実験の方法は、因子の数が2つ(シフトと機械)の二元配置実験になります。
【STEP 1】数値的な分析
二元配置実験では、まず平均値を水準の組み合わせごとに計算します。
表4 二元配置実験における水準ごとの平均値
表4で彩色した個所は、機械ごとの製品重量の平均値です。どの機械もほぼ同じ値で実用的に問題になる差ではありません。
表5で彩色した個所は、各因子の水準の組み合わせごとの製品重量の平均値です。組み合わせの平均値を見ることで、シフトと機械との交互作用を検証できます。交互作用とは、例えば、シフトの製品重量を見ると、昼勤の方が重いですが(昼勤500.21、夜勤492.34)、機械Aを使用したとき、ほぼ同じ重量(昼勤495.38、夜勤494.54)になっています。これは、昼勤が機械Aを使用するときに何らかの効果が作用した結果と考えられますが、この何らかの効果のことを交互作用と呼びます。
【STEP 2】視覚的な分析
二元配置実験の場合、平均値を計算した数表を折れ線グラフで視覚化します(図13)。
グラフを見ると機械Aの製品重量は、昼勤で最も低く、夜勤で最も高いことが分かります。交互作用の存在が示唆されますが、たまたま検査対象となった標本の結果です。全体においてもこの傾向が成り立つのか、統計的検定で検証します。
【STEP 3】検定
二元配置実験、すなわち因子が2つの場合の検定方法は2種類あります。この例のように組み合わせごとに繰り返しのある場合とない場合で、ない場合とは、例えば、昼勤で機械Aの製品重量を1回測定したような場合です。今回のケースでは、組み合わせごとに4回の測定を行っていますので、繰り返しのある二元配置分散分析を利用します。両者の違いは、交互作用の検定ができるか否かです。繰り返しのない場合、組み合わせごとの測定回数が1回となり反復の原則を満たしませんので、交互作用の検定ができません。
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- AIエージェントが代わりに働くようになったら人は何をするの?
- 永守氏がニデック完全退任、「経営者としての私の物語にピリオド」
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク
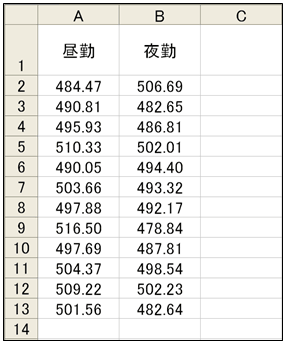 図8 Excelにデータを入力
図8 Excelにデータを入力![図9 ダイアログから[分散分析:一元配置]を選択](https://image.itmedia.co.jp/mn/articles/0810/30/mhfpro_doe02fig09.gif) 図9 ダイアログから[分散分析:一元配置]を選択
図9 ダイアログから[分散分析:一元配置]を選択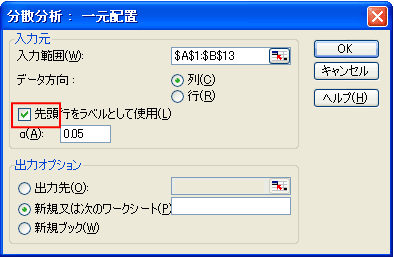 図10 出力オプションの決定
図10 出力オプションの決定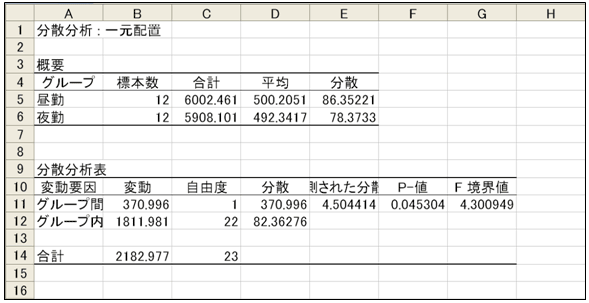 図11 計算結果
図11 計算結果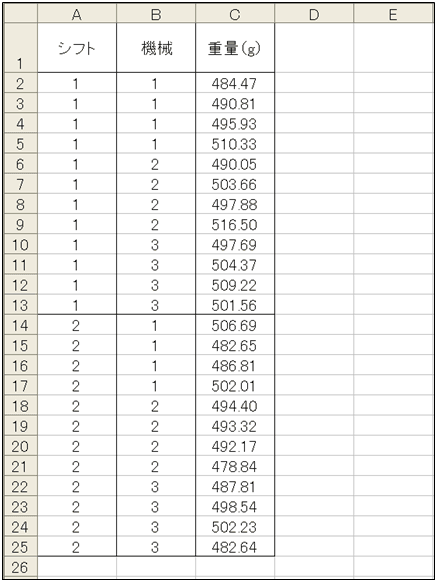 図12 機械という因子を追加したときのデータセット
図12 機械という因子を追加したときのデータセット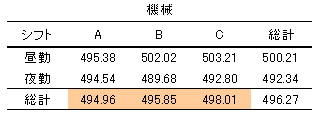
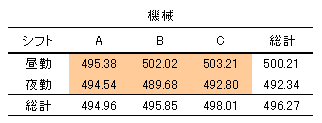 表5 二元配置実験における水準ごとの平均値
表5 二元配置実験における水準ごとの平均値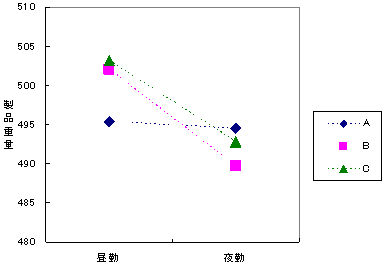 図13 二元配置実験の視覚的な分析
図13 二元配置実験の視覚的な分析



