エレクトロニクスを制する者は、カーエレを制す：知っておきたいカーエレクトロニクス基礎（3）（1/3 ページ）

カーエレを理解するには“エレクトロニクス”の知識が欠かせない。今回は自動車における電子制御回路について詳しく解説する。

[河合寿（元 デンソー） （株）ワールドテック，＠IT MONOist]

　これまでの連載で解説したとおり、カーエレクトロニクスの進歩を支えているのが“エレクトロニクス”の力です。

　そこで、今回は「カーエレクトロニクスに関する電子制御回路の基礎」をテーマに、各素子の特長に重点を置いて解説していきます。電子回路に出てくる各素子の定義やトランジスタ、CMOSFETなどの原理をマスターすれば、回路を理解するうえでの手助けになることでしょう。ちなみに、本テーマはかなりのボリュームとなりますので、今回と次回の2部構成でお届けします。

　さて、前編である今回は、回路および回路素子などの定義とその特長。そして、ダイオードとトランジスタについて解説していきます。自動車に関する直接的なお話とは少し離れてしまうように感じられるかもしれませんが、これを理解すれば、カーエレクトロニクスのことをより深く知ることができるでしょう。

回路素子と回路の定義

　はじめに、「回路素子」ならびに「回路」の定義について触れたいと思います。

　回路素子には“受動素子”と“能動素子”があります。受動素子とは、エネルギーを引き出すことができない、つまり増幅や発振などが行えない素子のことで、「抵抗」「コンデンサ」「インダクタ（コイル）」などがそれに該当します。

　一方、能動素子とは、適当な外部接続によってエネルギーを引き出すことができる、つまり増幅や発振などが行える素子のことで、「トランジスタ」「ダイオード」などがそれに該当します。

　次に回路の定義ですが、大きく“電子回路”と“電気回路”とに分類できます。前述の能動素子を使用した回路のことを電子回路といい、能動素子を使用していない回路のことを電気回路といいます。よく似ているようですが、このような違いがあります。

アナログとデジタルの定義

　続いて、カーエレクトロニクスによく出てくる“アナログ”と“デジタル”についても定義しておきましょう。

　アナログとは、連続的に変化する情報量のことで、“値”そのものに意味を持っています。音や光などの自然現象のほとんどがアナログといえます。

　一方、デジタルは数字がそのまま出てくるような量のことで、離散的な量しか表しません。その値が“H（High）”なのか、“L（Low）”なのかに意味を持ちます。

　ご存じのとおり、アナログ回路ではどうしても信号にノイズが入ってしまったり、ドリフトしたりして誤差が生じてしまいます。つまり、回路が多くなればなるほど誤差が積算されますので、アナログ回路はどちらかというと小規模回路向きといえます。

　これに対して、デジタル回路ではノイズが入ったり、ドリフトが生じたりしても、“信号がHなのか、Lなのかを判定すればよい”ものなのでその影響はあまり受けません。また、整形も簡単ですし、高精度の制御ができます。つまり、デジタル回路は大規模回路に向いているといえます。

　同じ機能を実現するだけでよければ、アナログ回路の方が回路規模は小さくて済みます。しかし、精度を取るならばデジタル回路の方がよいでしょう。いずれにせよ、回路規模や誤差の問題などを検討したうえで、その目的に合った実現方法を選択することが重要となります。

受動素子

　ここでは、受動素子である抵抗、コンデンサ、インダクタ（コイル）についてもう少し詳しく説明します。

抵抗

　抵抗に流れる電流と発生する電圧の関係は、「オームの法則」で求められます（式1）。抵抗Rは、電圧Vと電流Iとの“比例定数”となります。

V［V］ ＝ R［Ω］ × I［A］　……式1

　抵抗Rに電流Iが流れれば両端の電圧は「R × I」となります（式1）。逆に、両端に電圧Vが印加されれば、電流Iは「V ／ R」となり、電流が制限されたことになります。図1にその事例を示します。

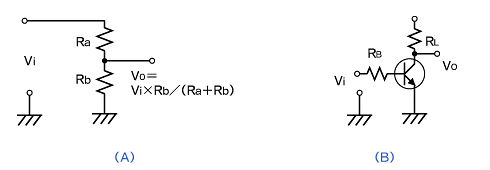図1　抵抗の回路事例

　図1（A）は、入力電圧Viを抵抗分割した回路です。抵抗RaとRbを流れる電流Iは式1から「Vi ／ （ Ra ＋ Rb ）」となります。Voは抵抗Rbの両端の電圧ですから「I × Rb」となりますので「Vo ＝ Vi × Rb ／ （ Ra ＋ Rb ）」となります。つまり、Voは抵抗RaとRbにより任意の電圧を得ることができます。

　図1（B）の抵抗は、トランジスタの“ベース電流”と“コレクタ電流”を制限した回路です。また、抵抗は後述のコンデンサやインダクタと違い、その抵抗値は周波数とは無関係です。抵抗の消費電力［W］は、「W ＝ V × I ＝ R × I² 」で求められ、この電力は“熱”となります。ちなみに、抵抗は自動車の電子制御回路でも頻繁に使用されています。

関連リンク：
	マザーボードで見る“抵抗器” http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_02.html
	リード線付き抵抗器のカラーコードを読む http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_03.html
	これだけは知っておきたい、抵抗器の種類 http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_04.html

コンデンサ

　コンデンサ（キャパシタとも呼ばれる）は2つの導体の間に電荷を蓄えるようにしたものです。図2に示すように導体の一方にQ［C：クーロン（電荷の単位）］、他方に−（マイナス）Q［C］の電荷を与えたとき、導体間の電位差をVとすると式2が成り立ちます。

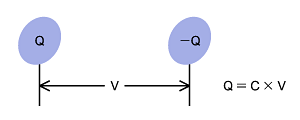図2　静電容量

Q ＝ C × V　……式2

　つまり、電荷Qと電位差Vとの比例定数が“静電容量”となります。従って、静電容量を有する素子がコンデンサとなります。コンデンサの基本は“電荷を蓄えること”ですが、さらにこれを交流回路に発展させますと次のようになります。

　電流は電荷の流れですから、「i ＝ dQ ／ dt」（dは微分記号）となります。これに式2を代入すると「i ＝ dQ ／ dt ＝ dCV ／ dt」となります。このVは交流ですから「v ＝ Vmsinωt」（Vm：最大振幅、ω：角速度で＝2πf（周波数）、t：時間）と表せます。これを基にすると、式3が求められます。

i ＝ dQ ／ dt ＝ C × dVmsinωt ／ dt ＝ ωCVmcosωt　……式3

　そして、インピーダンスZは“電圧（実効値）と電流（実効値）の比”ですから式4のようになります。

Z ＝ 1 ／ ωC ＝ 1 ／ （ 2πfC ）　……式4

　式3から、電流は電圧より90度位相が進んでいること示しています。また式4から、インピーダンスは周波数とコンデンサの静電容量に反比例することが分かります。つまり、周波数あるいは静電容量が大きいほどインピーダンスが小さくなり、周波数が高いほど電流が通りやすくなります。周波数を半分にした場合に、同じインピーダンスを維持するためには容量を2倍にすればよいことも分かります。ちなみに、この性質は「カップリングコンデンサ」「平滑回路」「フィルタ」によく使われます（図3）。

図3　コンデンサの働き

　また、スイッチではコンデンサに直流電圧を印加／遮断したり、パルスを印加する際に利用されます。この場合は抵抗とともに使用することになります。これは過度現象の理論で明らかにされています。その事例を図4に示します。

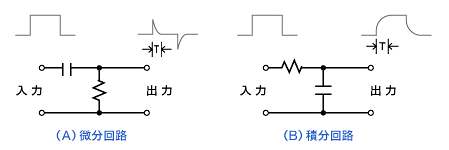図4　CRによる微分回路と積分回路

　図4（A）は微分回路、図4（B）は積分回路です。いずれも時間Tは「CR定数［sec］」で決まります。

関連リンク：
	コンデンサってどんなことをするの？ http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_05.html
	電解コンデンサが円筒状になっている理由 http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_06.html
	コンデンサの“容量値”を読む方法 http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_07.html
	押さえておきたいコンデンサの種類 http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_08.html