エレクトロニクスを制する者は、カーエレを制す：知っておきたいカーエレクトロニクス基礎（3）（2/3 ページ）

[河合寿（元 デンソー） （株）ワールドテック，＠IT MONOist]

インダクタ（コイル）

　インダクタ（コイル）とは、インダクタンスを持たせた素子です。図5（A）のようにコイルへ電流が流れると磁界が生じて、磁束はコイルと鎖交（コイル面と交わる）します。

---

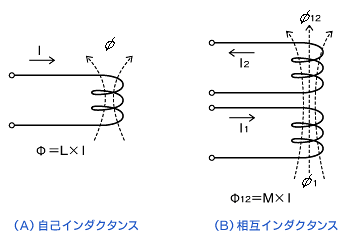図5　インダクタンス

　磁束ΦとΦが貫通する巻数の積の合計（鎖交したコイルの巻き数と磁束Φの積の和）を“磁束鎖交数Φ”といいます。このΦは式5に示すようにコイルに流れる電流Iに比例します。

注：Φは磁束の鎖交数、Φは磁束を示す。

Φ ＝ L × I［wb：ウエーバ］　……式5

　式5の比例定数L［H：ヘンリー］は、自己インダクタンス（普通インダクタンスと呼ぶ）と定義されます。

　回路が2つある場合を示したのが図5（B）です。一方の回路1に電流I1が流れるときに生ずる磁束のうち、磁束が回路2と鎖交しているときの磁束鎖交数をΦ12とすると、式6のようになります。

Φ12 ＝ M × I1［wb］　……式6

　この比例定数を相互インダクタンスといいます。一方、回路の電流が変化すると磁束鎖交数も変化しますので“ファラデーの法則（注）”に従って、回路に起電力を誘起します。図5（A）においては式7の起電力e1が、図5（B）においては式8の起電力e2が誘起されます。

注：ファラデーの法則とは、コイルに交わる（鎖交）磁束Φが変化すると、その変化する割合に比例した起電力（電気を流す働きをする力）がコイルに生じる現象のこと。

e1 ＝ −dΦ ／ dt［V］ ＝ −Ldi ／ dt［V］　……式7

e2 ＝ −dΦ12 ／ dt［V］ ＝ −Mdi1 / dt［V］　……式8

　回路が1つのときに交流を印加する場合には、e1の逆の電圧e（＝ −e1）が必要になります。ここでの電流は交流ですから「i ＝ Imsinωt」（Im：最大振幅）にすると、式9のようになります。また、インピーダンスZは式10になります。

e ＝ dΦ ／ dt ＝ Ldi ／ dt ＝ ωLImcosωt　……式9

Z ＝ ωL ＝ 2πfL［Ω］　……式10

　式9から電流の位相は、電圧より90度遅れていることが分かります。式10からインピーダンスは周波数およびインダクタンスに比例して大きくなることが導き出されます。この特性を利用して「ローパスフィルタ（LPF）（注）」や電源回路のノイズフィルタとして使用されています。また、コンデンサと同じくパルスを印加する回路もありますがコンデンサほど使用されていません。自動車用にはインダクタとしてよりも電磁力を発生するコイルとして、電磁弁やモータなどのアクチュエータに広く使用されています。

注：ローパスフィルタ（LPF）とは、低い周波数を通すフィルタのこと。

　相互誘導作用は原理的に無損失で、電圧を昇圧したり降圧したりするトランスとして幅広く利用されています。自動車用としては「昇圧用DC−DCコンバータ（注）」として使用されています。また最近では、電気自動車用のパワーデバイスとしても使用されています。

注：昇圧用DC−DCコンバータとは、低い電圧（12V）を高い電圧（例えば200V）に変換する回路のこと。

関連リンク：
	ま〜るい磁石にぐるぐる銅線、コイルの役割 http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_09.html
	2つのコイルが近づくと、何かが起こる!? http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_10.html
	コイルとコンデンサで引き起こされる“現象”とは？ http://monoist.atmarkit.co.jp/fembedded/elecatalog/elecatalog_11.html

各素子の複数接続

　次に、前述で解説してきた素子が複数接続された場合について考えてみましょう。

抵抗の複数接続

　抵抗の複数接続には、2個以上の抵抗を1列に接続した“直列接続”と、2個以上の抵抗の両端を同じ個所に接続する“並列接続”があります。また、この直列接続と並列接続を組み合わせた回路があります。

　直列接続された合成抵抗（最初の端子と最後の端子間の抵抗）は、式11となります。

R ＝ R1 ＋ R2 ＋ …… ＋ Rn［Ω］　……式11

　そして、並列接続された合成抵抗は式12となります。

R ＝1 ／ （ 1 ／ R1 ＋ 1 ／ R2 ＋ …… ＋ 1 ／ Rn ）［Ω］　……式12

コンデンサの複数接続

　コンデンサが直列接続された場合の合成静電容量は式13となります。

C ＝ 1 ／ （ 1 ／ C1 ＋ 1 ／ C2 ＋ …… ＋ 1 ／ Cn ）［F］　……式13

　コンデンサが並列接続された場合の合成静電容量は式14になります。

C ＝ C1 ＋ C2 ＋ …… ＋ Cn［F］　……式14

　このように抵抗とは逆の式になります。

インダクタの複数接続

　インダクタを直列接続した場合には相互誘導作用により相互インダクタンスがかかわってきます。2個の場合の合成インダクタンスは式15となります。

L ＝ L1 ＋ L2 ± 2M［H］　……式15

　＋（プラス）Mは2つのコイルの巻き方向が同じ（磁束が加わる）、つまり“和接続”の場合であり、−（マイナス）Mは巻き方向が反対（磁束が減じる）、つまり“差接続”の場合です。もちろん、2つのコイルから発生する磁束がお互いに影響しなければMは0となります。ちなみに、3個以上のインダクタの直列接続、あるいは並列接続することはほとんどありませんのでここでの解説は省略します。

　また抵抗、コンデンサ、インダクタを組み合わせて接続した場合を合成インピーダンスといいます。合成インピーダンスはベクトル計算で求められます。こちらについてもここでの解説は割愛します。ご興味のある方は交流回路の文献などを参照してください。