外部流れの熱伝達を理解する:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(17)(2/4 ページ)
自然対流熱伝達のシミュレーション
それでは、表1の条件に基づいて解析を行ってみましょう。図3にセル分割図を示します。乱流モデルはSST(Shear Stress Transport)です。
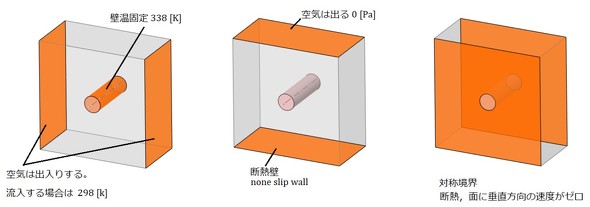
図4に、境界条件を示します。表1における伝熱界面温度は63.2[℃]ですが、切りのよい値として65[℃](338[K])にしました。
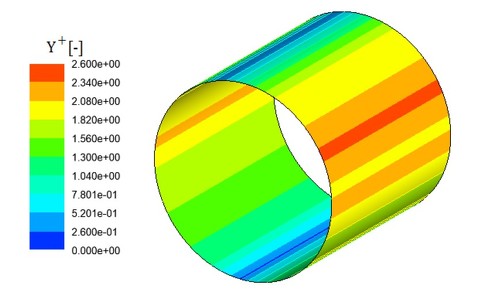
Y+(Yplus)をチェックしておきます。図5にその結果を示します。最大値が2.6[-]なのでOKです。
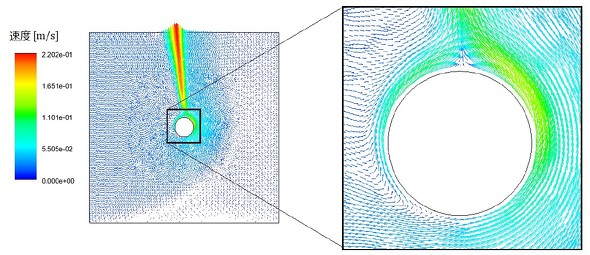
図6に、速度ベクトル図を示します。これは定常解析の結果ですが、なかなか左右対称になってくれません。後ほど時刻歴解析の結果を紹介しますが、そのアニメーションを見ると、上昇流が左右にゆらゆらと揺れている様子が確認できます。このことから、定常解析では左右対称にならないことが分かっていただけると思います。
図7に、壁面の熱流束分布を示します。伝熱界面における平均値は246.2[W/m2]でした。
動画1に、時刻歴解析による温度分布を示します。蚊取り線香の煙が二度と同じ形にならないのと同様に、この例でも温度分布は二度と同じにはならず、しかも左右非対称となります。
紙と鉛筆による計算結果とシミュレーション結果の比較:自然対流熱伝達
表1の計算結果はExcelによるものですが、ここではこれを「紙と鉛筆による計算」と呼びます。伝熱界面の温度を固定したので、比較すべきは伝熱界面の熱流束と熱伝達率となります。シミュレーションによる熱伝達率は、式8で計算しました。
表2に、熱流束と熱伝達率を示します。一致の度合いは、なかなか良好であるように思えます。実は、両者を近づけるためにセル分割を変更した解析を何度か実施しています。やはり、Y+の値が2〜3[-]以下になるまで、セル分割を細かくする必要がありました。
| 紙と鉛筆 | シミュレーション | ||
|---|---|---|---|
| 熱流束 | W/m2 | 265.3 | 246.2 |
| 熱伝達率 | W/m2.K | 6.946 | 6.155 |
| 表2 紙と鉛筆とシミュレーションの比較:熱流束と熱伝達率 | |||
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査



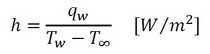 式8
式8





