機構制御系のモデリング(その1) 〜機構と制御の基本について考える〜:1Dモデリングの勘所(36)(3/4 ページ)
制御の基本
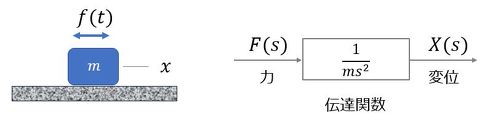
次に、摩擦のない床面に静止している質量mの物体に対し、外力f(t)が作用している場合の質点の運動を考える(図7)。
この質点の運動方程式は、
となる。この運動方程式を初期条件(t=0で変位、速度が0)の下、ラプラス変換すると式8となる。
これから、
となり、伝達関数は式10で定義できる。
次に、外力が作用したときの質点の応答について考える。外力の代表的なものとして図8に示す「ステップ入力」と「インパルス入力」を考える。
ステップ入力us(t)とは、ある時間(図8ではt=0)に、単位力が作用し、その後この状態が継続した状況である。一方、インパルス入力δ(t)とは、ある時間(図8ではt=0)に瞬間的に無限大の力が作用した状況である。δ(t)は「デルタ関数」といい、式11が成立する。
ステップ入力は物体をぶら下げた状態、インパルス入力は衝撃力を与えた状態で、いずれも日常的に経験する力の入力形態であり、ラプラス変換を用いることにより、これらの効果を表現、解析可能とする。通常の方法でこれらを模擬することは容易ではない。
図7について、力がステップ状に作用したときの質点の応答について考える。ラプラス変換の式を参考にすると、ステップ応答(ステップ入力に対する系の応答)は式12となる。
すなわち、ステップ入力を受けた静止した質点は、式12を時間で2回微分して、一定加速度1/mで運動することが分かる。
インパルス応答も同様にして式13で求まる。
すなわち、インパルス入力を受けた静止した質点は、式13を1回微分して、一定速度1/mで運動することが分かる。
このように、静止した質点にステップ入力、インパルス入力が作用すると、それぞれ一定加速度、一定速度で運動を開始して、次の外力が作用するまでこの運動を継続する。一般に、物体は何らかの外乱を受けるので、摩擦のない床面に静止している質点は制御の視点からいうと“安定ではない”ということになる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
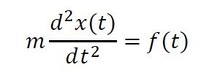 式7
式7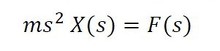 式8
式8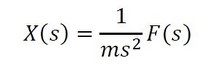 式9
式9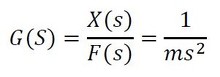 式10
式10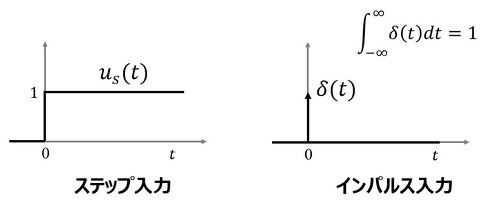
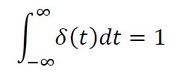 式11
式11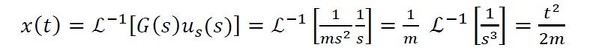 式12
式12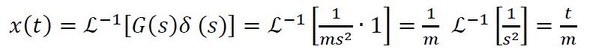 式13
式13





