吸音材と遮音材を使ったら騒音を何デシベル低減できる?:CAEと計測技術を使った振動・騒音対策(19)(2/5 ページ)
騒音のオーバーオール値
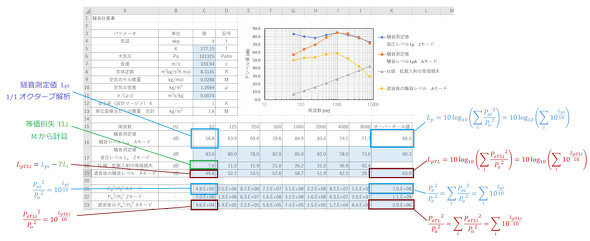
「結局、何デシベル下がるの?」という問いに対しては、騒音のオーバーオール値を答える必要があります。そのためには、全ての周波数の総和を計算する必要があります。この総和をオーバーオール値といいます。通常の騒音計が表示するのはオーバーオール値です。
表1の場合、63、125、250、500、1000、2000、4000、8000[Hz]の音圧の総和を求めることになります。では、周波数の異なる2つのsin波の和の実効値の二乗Pe2はどうなるか計算してみましょう。2つのsin波は次式とします。P1e、P2eは実効値です。
式2の第3項を考えましょう。次式となり、図3の積分となります。図3の下側のグラフに注目します。対称性がありますね。積分間隔Tをp1(t)の周期T1とp2(t)の周期T2の最小公倍数とすると、式2の第3項の積分はゼロになります。
よって、周波数の異なる2つのsin波の和の実効値の二乗は次式となり、それぞれのsin波の実効値の二乗の和となります。実効値の計算は連載第2回の式32を参照してください。
では、表1の測定値のオーバーオール値を計算しましょう。まず、デシベルの定義を式5、式6に示します。i=1が63[Hz]での値、i=2が125[Hz]での値とします。
遮音材による減衰後の音圧レベルは次式で求めます。
式6でそれぞれの周波数の音圧実効値(測定値)の二乗を求めます。式8でそれぞれの周波数の音圧実効値(遮音材による減衰後)の二乗を求めます。
次に式9、式10で実効値の二乗の和を求めます。
測定値と遮音材による遮音後の騒音レベルのオーバーオール値は次式となります。
これらの計算を行う「Excel」シートを図4に示します。これくらいであれば自分で作れるでしょう。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
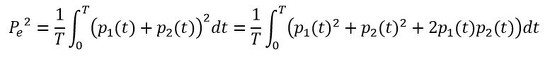 式2
式2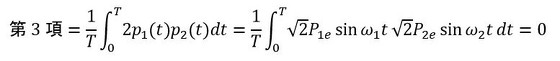 式3
式3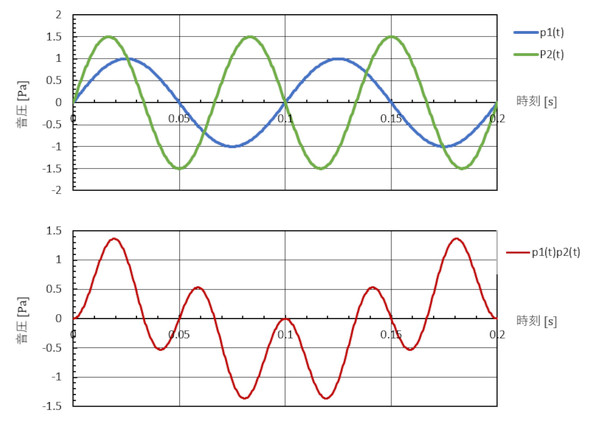
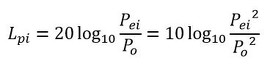 式5
式5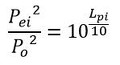 式6
式6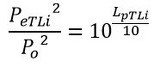 式8
式8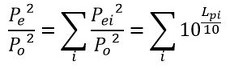 式9
式9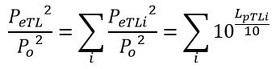 式10
式10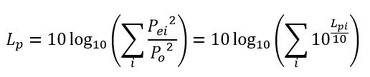 式11
式11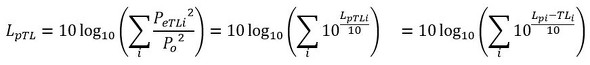 式12
式12