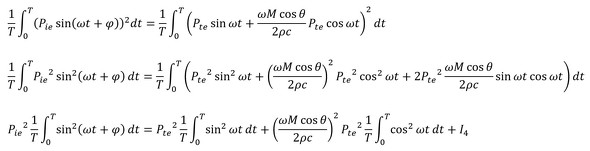騒音低減技術の基本「遮音」と「吸音」を理解する 〜遮音について〜:CAEと計測技術を使った振動・騒音対策(18)(2/5 ページ)
遮音の質量側
等価損失には垂直入射の等価損失TL0と拡散入射の等価損失TLがあり、設計の場面では後者を使います。等価損失は壁の材質で決まるのではなく、壁の質量で決まります。正確にいうと壁の1[m2]当たりの質量(面密度)で決定します。垂直入射の等価損失TL0は次式で求まります(参考文献[2])。
では、式4を導出しましょう。参考文献[2]には、板と空気の音響インピーダンスがz=jωMであることの説明がありませんので、いくつか筆者の解釈を加えます。垂直入射の等価損失を求めるために、平面音波が斜めから入射したときの等価損失を求めます。図5に遮音壁での音圧と粒子速度を示します。図5左図の青色で示した遮音材の微小面の運動方程式を立てます。運動方程式はf=mαでしたね。これに代入します。力fは「圧力×面積ΔS」です。運動方程式は次式となります。u0は微小面の面垂直方向の速度です。
「あれっ? 左辺の力にcosθを掛けないの!?」と一瞬思ったのですが、圧力はベクトル量ではなくスカラ量なのでcosθを掛ける必要はありません。
入射音、透過音は次式で表します。両者の位相が一致している保証はないので、pi側に位相角φを導入しました。Pie,Pieは実効値です。
連載第2回で大事な関係式を示しました。平面音波では粒子速度と音圧は比例関係で同一位相であるというものです。連載第2回で説明した粒子速度と音圧の関係式を以下に示します。
遮音材微小面の垂直方向速度は次式で表されます。pt側の音圧と同位相です。
式8を式5に代入します。
式9の右辺ですが、U0にωMが掛け算され、sinがcosに変わっています。これがインピーダンスz=jωMの意味ですね。微小面垂直方向の微小面の速度の連続性から次式が成立します。
式7を式10に代入し、ρc倍します。
式9と式11を足算して変形します。
微小面の微小面垂直方向の速度と透過側の圧力の関係は、平面音波であることを考慮すると次式が成立します。
式13を式12に代入します。
式14に式6を代入します。
式15を√2で割ります。
両辺を二乗し、1周期分だけ積分します。つまり、実効値の二乗を計算します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

 式4
式4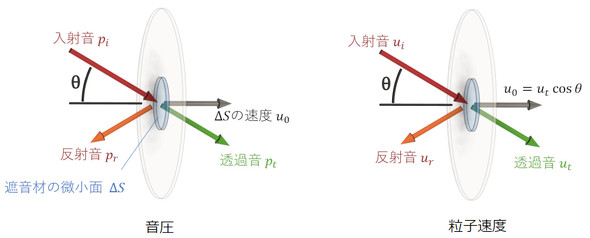
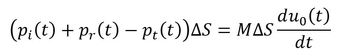 式5
式5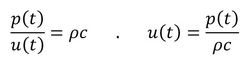 式7
式7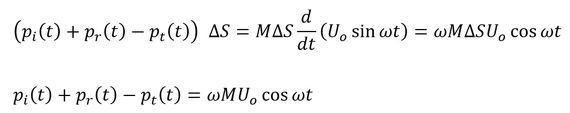 式9
式9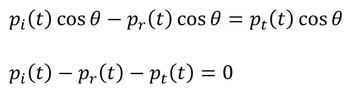 式11
式11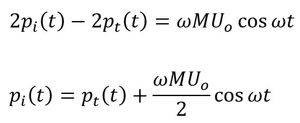 式12
式12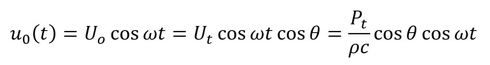 式13
式13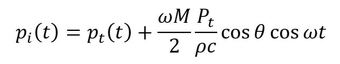 式14
式14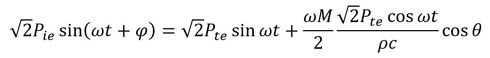 式15
式15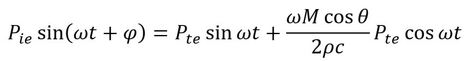 式16
式16