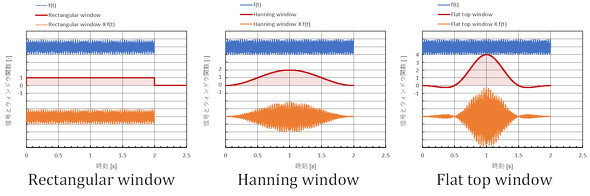
　FFTアナライザを使う際、「ウィンドウ関数」を選択しなければなりません。入力した時刻歴データに時間軸上でウィンドウ関数を掛け算して、その結果を高速離散フーリエ変換しています。ウィンドウ関数の例を図7に示します。青色が元の信号波形、赤色がウィンドウ関数、オレンジ色が信号波形にウィンドウ関数を掛けたもので、オレンジ色の波形を高速離散フーリエ変換することになります。

　「Rectangular window」は“何もしない”ということになります。「Flat top window」の赤色グラフをよく見てみると、マイナスの値を掛けており「おい、大丈夫か？」と思うのですが、なかなか良い性能を持っています。ウィンドウ関数は他にもありますが、それらは参考文献［1］［2］を参照してください。参考文献ではウィンドウ関数の最大値は「1」で統一されていますが、ここではピンク色の領域の面積が等しくなるようにウィンドウの大きさを調整してあります。

図7　ウィンドウ関数［クリックで拡大］

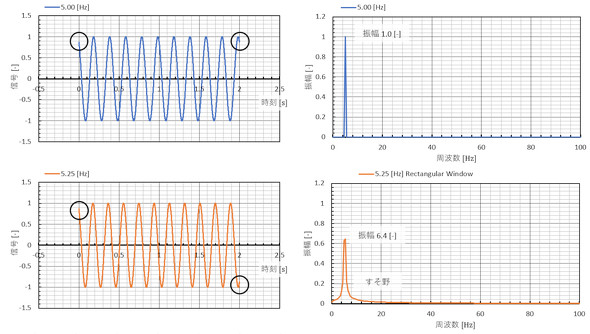
　では、単一周波数で振幅1［-］のsin波を周波数分析してみましょう。まずはRectangular windowで、図8に示します。上段は5.00［Hz］、下段は5.25［Hz］です。5.00［Hz］の場合は振幅1.0［-］との結果となりましたが、5.25［Hz］の場合は振幅6.4［Hz］で裾野が広がりました。上段と下段の違いは黒丸（○）で示した信号の最初と最後の値です。上段の信号の最初と最後の値は等しく、下段は異なる値です。

図8　単一周波数のsin波の周波数分析：Rectangular window［クリックで拡大］

　図9は下段のサンプリングデータを2セット分つなげたものです。つなげた部分で不連続な信号となっています。下段の場合はこのような信号を周波数分析していたことになっており、不連続部が影響を及ぼしていたと解釈できます。

図9　サンプリングデータを2セット分つなげたもの 5.25［Hz］［クリックで拡大］

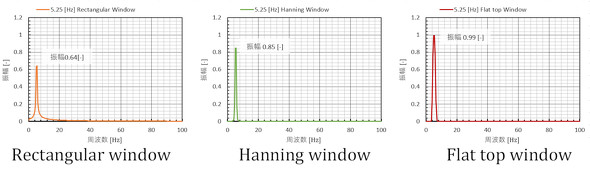
　それでは、ウィンドウ関数を掛けて、この不連続な信号を周波数分析してみましょう。「Hanning window」とFlat top windowでは裾野がなくなり、Flat top windowに至っては振幅が0.99［-］と元の信号の振幅となりました。

図10　単一周波数のsin波の周波数分析結果［クリックで拡大］

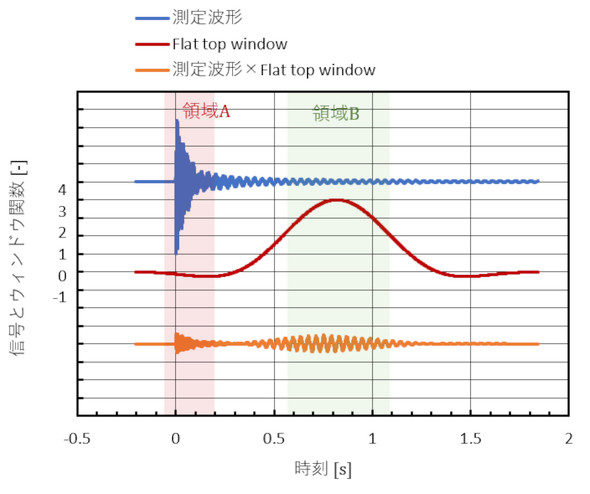
　続いて、Flat top windowが万能かどうかを調べてみましょう。図11は間欠的な加速度波形にFlat top windowを掛けたものです。領域Aに意味がありそうなので、ここを分析したいのですが、Flat top windowを掛けると、領域Aの信号にマイナスの小さな値が掛け算されて小さくなってしまい、なおかつ見たい信号の位相が反転してしまいました。

　領域Bの信号に対しては、Flat top windowを掛けたことにより大きくなっているので、周波数分析結果は領域Bの信号の影響を大きく受けることになります。領域Bの信号はおそらく、最も低い周波数成分が減衰せずに残っている部分で、「意味がない」とは言いませんがここの信号からは多くの情報は得られないでしょう。

　以上のことから、間欠的な振動や騒音を周波数分析するときは、Rectangular windowしか選択肢はありません。もし、どうしてもウィンドウ関数を使いたいのであれば、うまくトリガ条件を設定して意味のある信号だけをサンプリングし、そして波形を注意深く観察してウィンドウ関数を選ぶ必要があります。

　大切なことは、FFTアナライザのデフォルト設定でどのウィンドウ関数になっているかであり、測定前に必ず確認しておきましょう。