標準偏差って何? 公差設計で生産バラツキを統計学的に考える:3D設計推進者の眼(30)(2/3 ページ)
正規分布とヒストグラム
さて、少し頭の痛くなる話ですが、「正規分布」のお話をしましょう。
私が正規分布を勉強したのは、高校生の時、当時は「数IIB(今は「数B」)」といわれる数学の教科書の中で勉強しました。理系専攻の私でしたが、あまり理解できていなかったと記憶しています。その私が正規分布の話をするのですから、当時の数学の先生もびっくりでしょうし、私自身も滑稽な感じもしますが、製造業に勤めることで、測定値や寸法値といったものが身近にあったのでその理解も進み、また“公差計算・公差解析”の用途として、その価値を感じるようになりました。
ということで、“バラツキを統計学的に考える”という意味での正規分布の話を始めることにしましょう。
上図のような形状の部品があります。設計上、段差形状の部分になる赤線枠内の寸法管理が必要です。この部品を100個切削加工したとし、その時全数検査を行ったこととしましょう。
この結果をまとめるために、ヒストグラムを作成します。補足ですが、“ヒストグラム”は、棒グラフとは表す意味が異なります。棒グラフはその棒1本ごとの比較をします。どの棒が長くてどの棒が短いか、例えば、棒の長さが個数を示しているのであれば、どれが多くてどれが少ないかの比較をします。一方でヒストグラムは、全てに対して分布を見るもので、「どこに分布が集中しているのか」「どこに分布がないのか」を見るものです。
このヒストグラムから見て分かることは、データ区分「10.00mm」が最も大きくなり、そこを中心にしてその外側の大きさが徐々に徐々に小さくなっていくという左右対称となる分布の形となっていることです。
では測定部品数とその測定値を区分したデータ区分が狭くなるとどうでしょうか。
この例では、生産部品数(測定部品数)を100個から200個の2倍に、データ区分を0.50mmから0.25mmの2分の1にしてみました。そうすると、測定部品数100個の場合と同様に、最も大きい分布を中心として、その中心の外側に向けて徐々に減少する形でありながら、山の大きさが細分化されて、なだらかになっていくことが分かります。
私の経験では、量産型で、安定的な加工が行われている部品の寸法測定の場合では、このような左右対称型のヒストグラムの形になります。個別受注生産型製品を構成する部品寸法の測定では、ここまでの測定部品数を得ることは、長期間にわたり、現実的には難しいかもしれませんが、都度、部品の測定値を蓄え続けていくと、はじめにお話したような“一様分布”になることが、経験的に示されています。
ヒストグラムのタイプ
ここで、“左右対称型”というヒストグラムの形についてお話ししましたので、もう少しヒストグラムの形のタイプについて、部品加工の際の寸法測定を対象にして、その特徴の説明をしましょう。
ヒストグラムの形には次のようなタイプがあります。
- 一般型・左右対称型:最も見られる形。平均値をヒストグラムの中心とした左右対称型が見られる時には、工程は安定している。
- 離れ小島型:工程もしくは測定に異常があった可能性あり。
- ふた山型:平均値が異なるデータが混在したことによる。異なる作業者、異なる機械のデータが混在している可能性あり
- 歯抜け型:データ数が少ないか、データ区間の設定が適切でない場合に見られる。測定器の問題、測定器の見方(測り方)でも生じることがある。
- ゆがんだ型(左または右絶壁型):規格外のデータを含めなかった可能性がある。極端に左右のどちらかに偏っているような場合もあり、必ずしも異常とはいえない。
ヒストグラムから、このような状態が推測できることも面白いと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
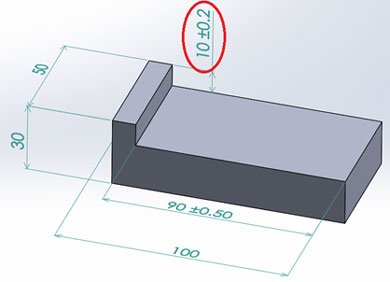 モデルケース
モデルケース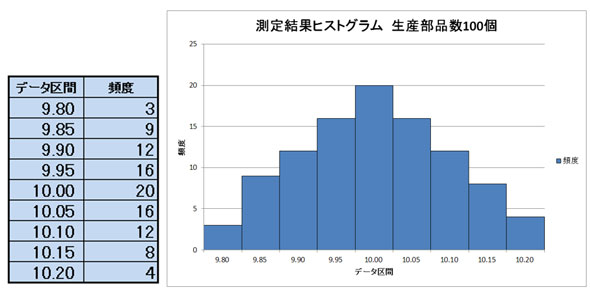 測定結果のヒストグラム 測定部品数100個
測定結果のヒストグラム 測定部品数100個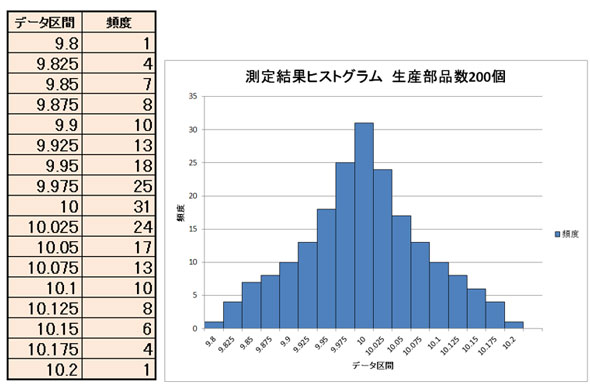 測定結果のヒストグラム 測定部品数200個
測定結果のヒストグラム 測定部品数200個





