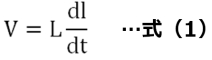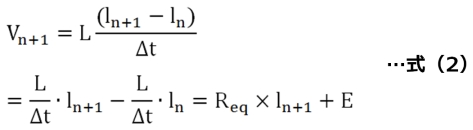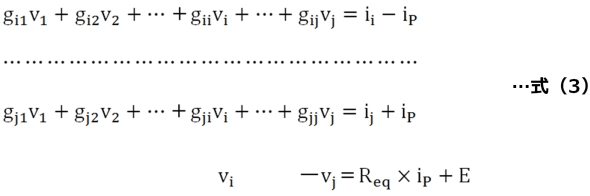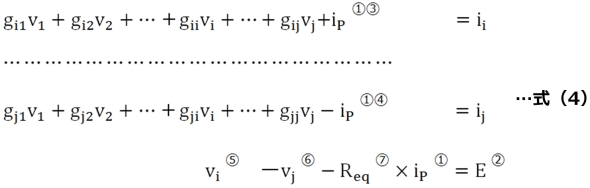SPICEの過渡解析（その2）：インダクタンス素子の場合：SPICEの仕組みとその活用設計（5）（1/4 ページ）

SPICEの過渡解析では、第4回で紹介したキャパシタンス素子の他に、インダクタンス素子も対象となる。第5回では、このインダクタンス素子を用いた回路の過渡解析について取り上げる。また、理想電圧源の組み込みについても説明する。

[加藤博二（Sifoen），MONOist]

　前回は電子回路で使われるキャパシタ（キャパシタンス素子）の過渡解析について説明させていただきましたが、前進法と後退法の特徴についてはご理解いただけたでしょうか？

　今回は電子回路で使われるもう1つの非定常素子であるインダクタンス素子の解析について説明します。インダクタンス素子はインダクタ、L素子とも呼ばれ、単体として使われる他、トランスの等価回路にも頻繁に使われています。

　そして今回は、連載第2回でお約束した通り、理想電圧源の組み込みについても説明します。

インダクタンス素子（インダクタ）

　インダクタLを流れる電流Iと誘起電圧Vの関係は式（1）で示されます。

　キャパシタのときと同様に後退差分法を使って、この微分方程式を刻み時間Δtで差分化すると式（2）になります。ここでV_n+1はΔt経過後の電圧値です。

　ここでReqは等価抵抗、Eは等価電圧源であり、次のように定義されます。

　このR_eqは抵抗単位ですが、コンダクタンス単位にするため単純に1/R_eqにしただけではL＝0を代入した場合に無限大のコンダクタンスとなって計算が破綻してしまいます。ですので、この方法ではインダクタを回路要素行列［G］に組み込むことはできません。

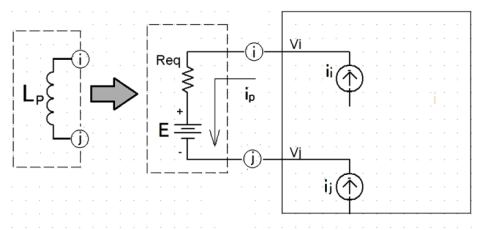
　ここでは一度、回路要素行列を作成した時の図1に戻って定式化を考えます。節点ij間にP番目のインダクタL_Pが接続された時の状況は図1の通りです。

図1　インダクタ接続図（クリックで拡大）

　この時、図1の各節点では節点iから電流i_PがインダクタL_Pへ流れ出し、リターン電流が節点jに流れ込んでいることが分かります。

　この電流i_Pを考慮すると、回路方程式は次のように修正されます。

　この式（3）のi_Pを左辺へ移項すると、

となって、等価電圧源Eと抵抗R_eqを組み込み込んだ新しい回路要素行列を得ることができます。

　以上をまとめると、インダクタ組み込みのための定式化の法則は次の通りになります（式（4）中の丸付き数字は、次の定式化の手順番号と対応します）。

①　電圧ベクトル［V］の末尾にインダクタの電流i_pが入る
②　電流ベクトル［I］の末尾にインダクタの等価電圧Eが入る（式（2）参照）

　そして各行列要素は次のようになります。

③　g（i,m＋p）＝1（1列拡張し、i行に＋1）
④　g（j,m＋p）＝−1（拡張された列のj行に−1）
⑤　g（m＋p,i）＝1（1行拡張してi列を＋1）
⑥　g（m＋p,j）＝−1（拡張した行のj列を−1）
⑦　g（m＋p,m＋p）＝−R_eq（L）（拡張マトリックスの対角末尾に−R_eq）

　ここでmは、従来の回路要素行列の最大要素数であり、Pは追加されたインダクタの順番を示す番号です（図1のR_eqとEの接続点はインダクタの等価回路ですので節点番号は不要です）。

　インダクタが複数個ある場合は行列の要素数を都度、増やしていくことになります。