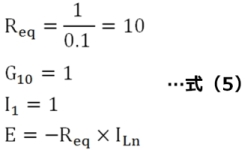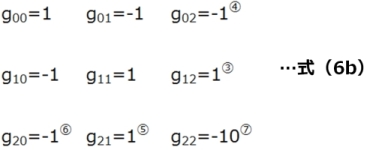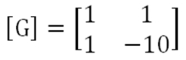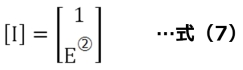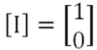SPICEの過渡解析（その2）：インダクタンス素子の場合：SPICEの仕組みとその活用設計（5）（2/4 ページ）

[加藤博二（Sifoen），MONOist]

過渡現象解析事例

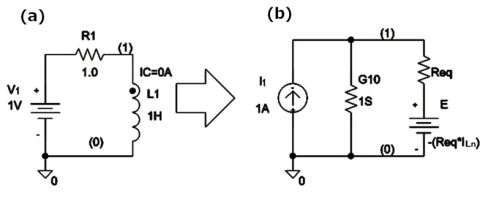
　実際の解析事例として図2（a）のLR回路を取り上げ、時刻0において電源V₁が接続された時の各部の電圧、電流の変化の様子を求めます。

• 条件1：初期条件としてインダクタL₁の電流は0Aとします
• 条件2：解析の時間ステップは0.1秒間隔で1秒間の解析を行います

図2　LR回路（クリックで拡大）

　等価回路は図2（b）に示すようになります。

• V₁とR₁（1Ω）⇒I₁とG₁₀
• L₁（1H）⇒R_eqとE
• 時間刻み⇒0.1秒

　これらを上記の定式化のルールに従って回路要素行列［G］を組み立てると各要素の定数は次のようになります。

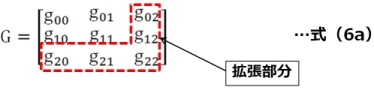
　従って、回路要素行列［G］は、本来の節点番号0,1からなる2行2列を拡張した式（6a）の3行3列の行列になります。

　ここで、具体値を代入すると式（6b）のように値を決めることができます（式（6b）内の丸数字は定式化の手順番号です）。

　ここから0行と0列に関する要素を抜くと、解くべき回路要素行列［G］は、

となります。

　そして、電流ベクトル［I］は、

となります。

　初期値としてI_L0＝0を与えると、E＝−R_eq×I_L0＝0ですので、電流ベクトルの具体値は

となります。つまり、この行列を解けば式（8）のように各値を得ることができます。

　この値は、初回刻み時間Δtが経過したときの各節点値です（この例では0.1秒後）。このようにして新しい節点1の電圧v₁、インダクタ電流i_L1が求まりましたので、式（5）のインダクタ等価電圧E（＝−R_eq×I_Ln）を更新して電流ベクトル［I］を組み直し、上記と同様に解けば計算を進めることができます。

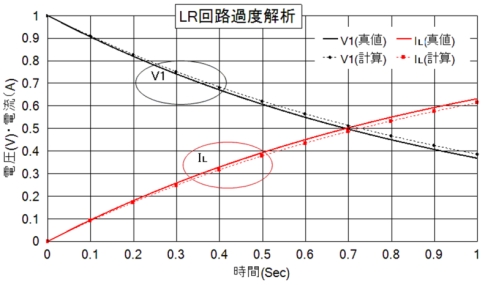
　この繰り返しの結果を図3に示すとともに、参考として代数学的な真値も併記します。1次近似でかつ、粗い刻み時間ですので真値とは差を生じていますが、現象そのものは再現できています。

図3　LR回路応答波形（クリックで拡大）