スライダー穴を工夫して、計画通りの動作でニヤリ:メカメカリンクで設計しよう(9)(1/2 ページ)
リンクとスライダー、どちらから操作しても狙った動作ができる機構、動作を止めたいところで止める機構の紹介。計画通りの動きに、ニヤリとしよう。
今回はスライダー穴の形状を工夫したスライダークランク機構を紹介します。スライダーの穴に工夫を凝らすとは、単純な直線形状の長穴にするだけでなく直線と曲線を組み合わせたり、長穴を傾けたりさせて設計することです。どんなユニークな動作ができるかを確認しましょう。
【No.34】スライダーの変形穴を利用した片側停止クランク 1
スライダーが左端の死点位置にあるとき、駆動リンクが連続回転しているにもかかわらずスライダーが一時停止する機構です。
変形穴の円弧部分の領域では駆動リンクが回転運動を続けているにもかかわらずスライダーは停止し、円弧部以外ではスライダーが平行移動するという間欠スライド動作を実現します。
駆動リンクが回転しているにもかかわらず、スライダーが停止する領域を「不感帯」と呼びます。
【No.35】スライダーの変形穴を利用した片側停止クランク 2
スライダーが右端の死点位置にあるとき、駆動リンクが連続回転しているにもかかわらずスライダーが一時停止する機構です。No.34の変形穴を左右反転させたものです。
間欠動作をさせる場合は、図3のように駆動リンクの回転支点を中心とした同心円を描き、動作し始めるポイントで直線、あるいは曲線とをつなげばよいのです。
駆動リンクの回転スピードが極低速の場合、円弧とその他の線との接続部にエッジを残して線を接続すると、「カクッ」という感じでシャープな動作をさせることができ、接続部に大きなRで線をつなげると「ジワッ」という感じでマイルドな動作をさせることもできます。このあたりの形状で動作をチューニングすることができるのです。
カムを用いた機構
前述のように間欠動作ができるのは、スライダーの変形穴にカム構造を仕込んでいるからです。
カムを用いた機構とは、任意の形状を持ったカム面に沿わせて、接触する相手部品に任意の運動を与える機構です。2次元動作を行う平面カムと3次元動作を行う立体カムに大別できます。カムを使った身近な製品に、自動車のエンジンで吸排気バルブの開閉に使われるカムシャフトがあります。カムの形状(カムプロファイル)が、バルブの開閉タイミングや開閉時間を変化させ、エンジンの馬力やトルク特性などに影響を与えます。
カム機構の特徴として、次のようなものがあります。
- 任意の運動を相手部品に与えられる
- 速度や加速度を連続にすることができるため衝撃が少なく低騒音である
- 高速動作に耐え、安定した動作を得られる
- 簡潔な動作の場合、機械的なシーケンス制御が可能であり電気的な制御を必要としない
【No.36】スライダーの長穴を利用したクランク機構 1
駆動リンクの回転によって、スライダーを平行移動させる機構です。長穴をスライダーの移動方向に対して直角にレイアウトすることで、駆動リンクを回転させ、スライダーを連続平行移動させます。
【No.37】スライダーの長穴を利用したクランク機構 2
駆動リンクの回転によって、スライダーを平行移動させる機構です。長穴をスライダーの移動方向に対して傾斜を持たせてレイアウトすることで、駆動リンクの回転によってスライダーが連続平行移動します。
回転する駆動リンクが入力の場合、No.36とNo.37に大きな違いはありません。それではなぜ、No.37のようにスライダーの長穴を傾ける必要があるのでしょうか?
入力をスライダー側から与えた場合を考えてみましょう。No.36のレイアウトにおいて、長穴の側壁が回転リンクと直角位置になる位置(死点=デッドポイント)では、スライダー側から入力できません。
No.37のように長穴を傾けることによって、全ての位置でスライダー側からの入力方向に対して回転リンクにモーメントを与えられる関係を作ることができるのです。これを「可逆特性」と呼び、「入力側からも出力側からも動作可能なこと」を示します。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
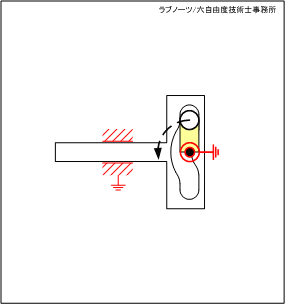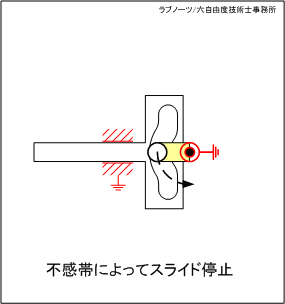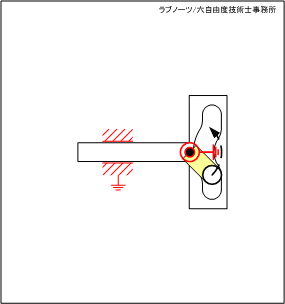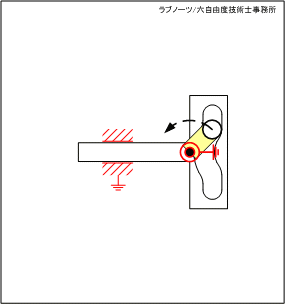 図1 スライダーの変形穴を利用した片側停止クランク 1
図1 スライダーの変形穴を利用した片側停止クランク 1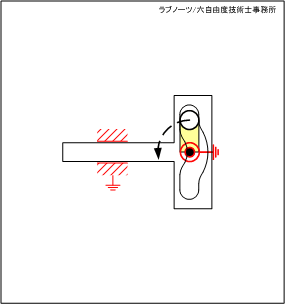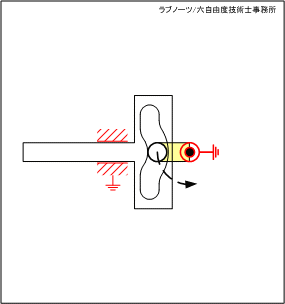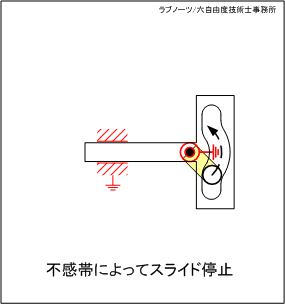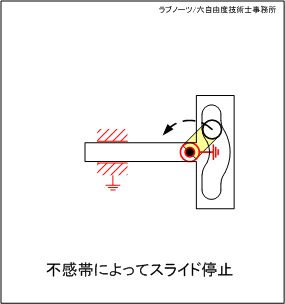 図2 スライダーの変形穴を利用した片側停止クランク 2
図2 スライダーの変形穴を利用した片側停止クランク 2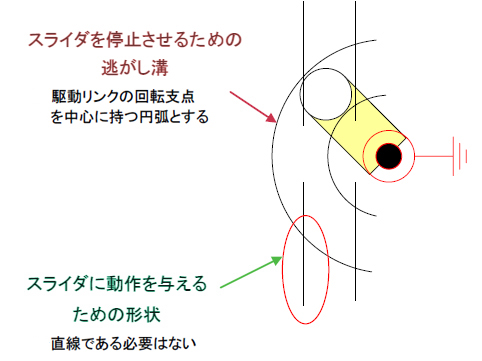 図3 不感帯を発生させる円弧穴の設計
図3 不感帯を発生させる円弧穴の設計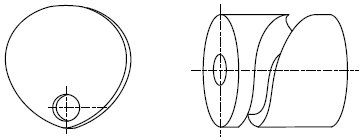 カムの種類
カムの種類 自動車のエンジンに使われるカム
自動車のエンジンに使われるカム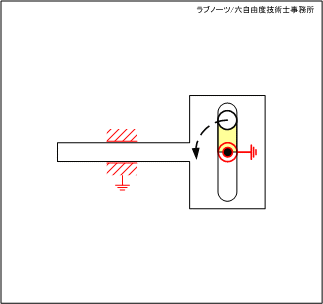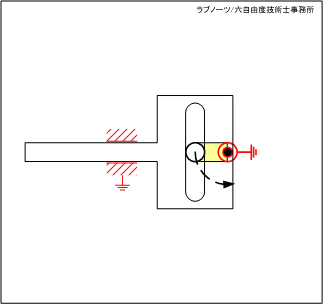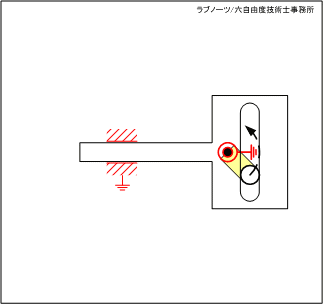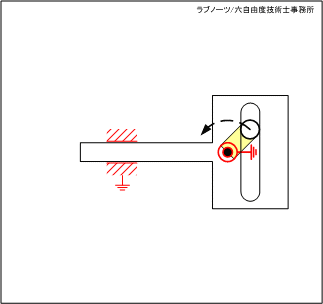 図4 スライダーの長穴を利用した回転クランク機構 1
図4 スライダーの長穴を利用した回転クランク機構 1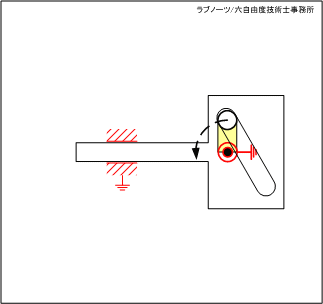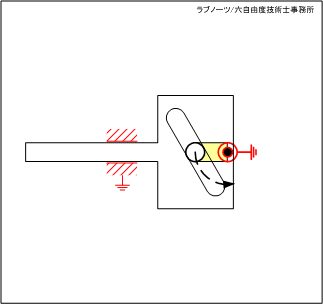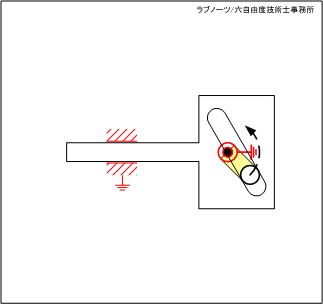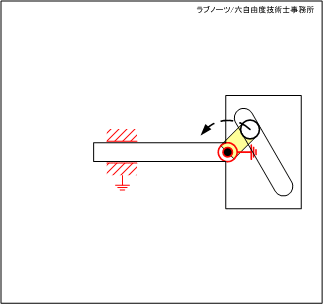 図5 スライダーの長穴を利用した回転クランク機構 2
図5 スライダーの長穴を利用した回転クランク機構 2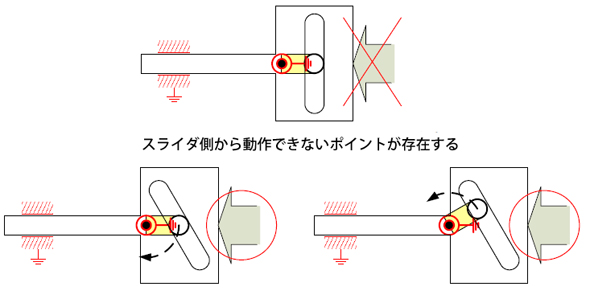 図6 機構の可逆性
図6 機構の可逆性





