滑らかで安定したライントレースを実現する:ETロボコンではじめるシステム制御(4)(1/2 ページ)
今回は実際に走行体(教育用レゴ マインドストームNXT)にPID制御を適用し、滑らかなライントレースを実現するまでの手順を解説
前回「オンオフ制御の欠点を補う『PID制御』とは?」では、PID制御を理論面から紹介しました。P制御、I制御、D制御がそれぞれどのように操作量に影響を与えるかを理論面から理解できたと思います。
いよいよ今回は、実際の「教育用レゴ マインドストームNXT(以下、走行体)」にPID制御を適用して、滑らかなライントレースを実現するまでの手順を解説していきたいと思います。
まず、走行体にPID制御を適用するためにプログラムを準備します。また、併せて、P、I、Dの各制御がどのようなプログラムになるかも解説していきます。
1.PID制御をプログラムへ
前回説明したとおり、PID制御ではKp、Ki、Kdの3つのパラメータを用います。
下記(図1)のプログラムはセンサー値と目標値から操作量を返す関数で、PIDの各制御の項がプログラムのどの部分になるかを示しています。ロボコンの走行体においては左右に旋回することでセンサー値を目標値に近づけますので、求めた操作量はバランス制御APIの旋回命令値に指定します。
P制御
図1の16行目がP(比例)制御についての記述です。Pは定数×偏差ですから、プログラムでは偏差を“センサー値 − ターゲット値”として求め、これに定数Kpを掛けてP値を求めています。
I制御
17行目がI(積分)制御についての記述です。Iは定数×偏差の積分です。プログラムでは14行目で偏差の積分をintegralに取っています。連続的にセンサー値を取り続けることはできないので、このPID処理が呼ばれる周期をDELTA_Tとし、これが十分短い時間であるとして近似し、偏差の積分を求めています。こうして求めたintegralに定数Kiを掛けてIを求めています。
D制御
18行目がD(微分)制御についての記述です。Dは定数×偏差の微分ですから、最新の偏差から前回の偏差の差を時間で割り、近似的に微分を行って定数Kdを掛けています。
これで、走行体にPID制御を適用するためのプログラムはあらかた完成しましたが、最後に1点、ひと工夫が必要です。それが20行目で行っている、操作量の最大値・最小値を制限する関数の呼び出しです。
これはバランス制御(balance_control)APIに与える旋回命令値の最大・最小値がそれぞれ−100、100であるため、これを超えるような値を旋回命令値として、バランス制御APIに渡すことを防ぐために必要な処理です。
バランス制御APIには、旋回命令値と同様に、前進命令値として−100〜100の間の数値を渡せますが、今回は固定値(100)とします。これは、旋回命令値を求めるために最適なPIDパラメータが前進速度によって変化するためです。皆さんが、コースによって速度を変化させながらPID走行を行う戦略を採用する場合には、それぞれの速度に適したPIDパラメータを使用することをお勧めします。
これにてPID制御のプログラムについての説明は終わりです。思った以上に単純なプログラムで拍子抜けしたかもしれませんが、その分、プログラムの内容については皆さんに十分理解してもらえたかと思います。
次は、このプログラムに設定するPIDパラメータKp、Ki、Kdを求めていきます。
2.PIDパラメータを求める ― 限界感度法 ―
これからPIDパラメータを決めていくわけですが、いくら各PIDパラメータの意味を理解していたとしても、トライアンドエラーでゼロから調整していくのは、とても大変で、時間のかかるプロセスであることは容易に想像できるかと思います。
そこで目安となるPIDパラメータを求め、それをチューニングしていくという手順を踏みたいと思います。いくつか方法がありますが、今回は「限界感度法」という方法でPIDパラメータを求めていきます。一般的な方法と少し異なる部分がありますが、目安としては十分です。
限界感度法では、P制御とI制御、D制御を関連付けた下記のパラメータを使用しますので、これを先に説明します。
Tiは積分時間で、KpをTiで割ることでKiを求めることができます。また、Tdは微分時間で、KpにTdを掛けることでKdを求めることができます。つまり、Kpを基準値として、Ki、Kdを求めていくことになります。なお、今回はPIDパラメータKp、Ki、Kdを求めることが目的であるため、Ti、Tdの詳細な意味については割愛します。
限界感度法では、まずP制御のみで動作させて、P制御の係数Kpを徐々に大きくしていきます。すると偏差に対する制御量が大きくなっていきますから、ある値でオーバーシュートが収束せず振動が持続するようになります。この値を限界感度と呼び、以降Kuで表記します。
図2はKpがKu未満、Kuに等しい、Kuより大きい場合のイメージです。
図2のグラフからも分かるように、KpがKuよりも小さい(制御が足りない)場合は、次第に振動収束し、KpがKuよりも大きい(制御が強過ぎる)場合は、次第に振動が発散していきます。
下に示すグラフ(図3)は、実際にKpを変化させて走行させたときのセンサー値のグラフです。図2のグラフのようなきれいな波形を描けていませんが、Kp=0.6より大きくするとコースアウトし、限界感度を超えたと考えられること(注1)から、Ku=0.6として計算を行っていきます。
なお、図3では0.2刻みのKpの波形しか示していませんが、実際は限界感度付近ではもっと細かくKpを変化させながら、Ku値を求めています。皆さんがKu値を求める場合にも、限界感度付近で細かくKpを変化させることをお勧めします。
また、走行体のモータ特性などにより走行体ごとにKu値は異なるため、皆さんがお持ちの走行体を用いて取得したKu値は、今回わたしたちが求めたKu値とは異なるかと思います。ですので、皆さんがお持ちの走行体を用いてKu値を求めることをお勧めします。
グラフだけでは少し分かりにくいでしょうから、Kp=0.6のときの走行を映像として示します(動画1)。持続振動している状態が分かるかと思います。
また、映像からは分かりにくいですが、以下(図4)のように目標値より少し明るい所にずらしてスタートしています。こうすることで、走行体に対し外乱を与え、走行体の走行に振動状態を発生させるようにしています。
Ku値を求めることができたら、今度はこのときの振動の周期も計測します。この周期をPuとして、以下の計算に使用します。それでは、求めたKu=0.6、Pu=0.6(600ms)を、限界感度法によるPIDパラメータKp、Ki、Kdの算出計算式に当てはめて、PIDパラメータを求めていきましょう。
まずは、Kp、Ti、Tdの値を求めます。
| Kp | Ti | Td | |
|---|---|---|---|
| 計算式 | 0.6×Ku | 0.5×Pu | 0.125×Pu |
| 計算結果 | 0.36 | 0.3 | 0.075 |
上で求めた計算結果を使用して、Kp、Ki、Kdの値を求めます。
| Kp | Ki | Kd | |
|---|---|---|---|
| 計算式 | − | Kp/Ti | Kp×Td |
| 計算結果 | 0.36 | 1.2 | 0.027 |
これでようやくPIDパラメータKp、Ki、Kdの目安値が求められました。それではこの数値をプログラムに適用して走らせてみましょう(動画2)。
残念ながら、いきなりコースアウトしてしまいました。走行体や測定条件によって異なるため、皆さんの求めたPIDパラメータを使用した走行ではコースアウトしなかったかもしれません。
しかし、求めたPIDパラメータそのままでは走行が不安定であったり、ムダな走行が発生したりしているのではないでしょうか? このままでは、滑らかなライントレースとは程遠い状態ですので、ここからは限界感度法で求めたPIDパラメータをベースにして、走行体の走行状態からPIDパラメータをチューニングしていき、滑らかなライントレースを行うための最適なPIDパラメータを求めていきたいと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 出荷量1.3倍を実現、電源不要のIoTゲートウェイが南種子町にもたらす農業改革
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
コーナーリンク
 図1 センサー値と目標値から操作量を返す関数
図1 センサー値と目標値から操作量を返す関数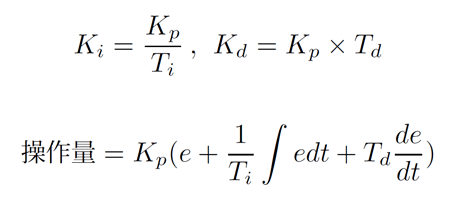
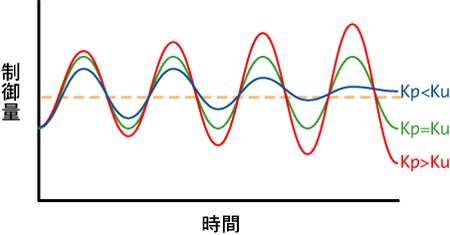 図2 KpがKu未満、Kuに等しい、Kuより大きい場合のイメージ
図2 KpがKu未満、Kuに等しい、Kuより大きい場合のイメージ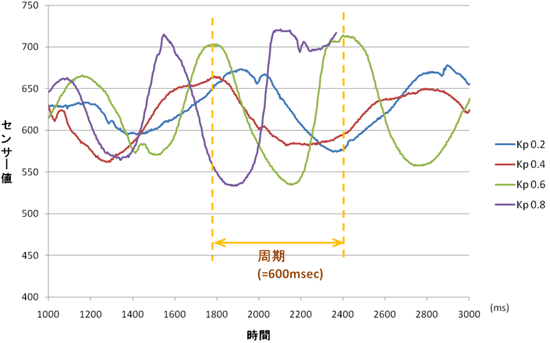 図3 Kpを変化させて走行させたときのセンサー値のグラフ
図3 Kpを変化させて走行させたときのセンサー値のグラフ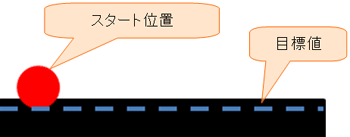 図4 目標値より少し明るい所にずらしてスタート
図4 目標値より少し明るい所にずらしてスタート

