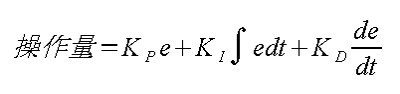オンオフ制御の欠点を補う「PID制御」とは？：ETロボコンではじめるシステム制御（3）（1/2 ページ）

今回は、前回紹介した「オンオフ制御」の欠点を克服するために、「PID制御」の導入を理論面から検討する！

[久納 工（永和システムマネジメント），MONOist]

　前回「オンオフ制御によるライントレースに挑戦」では、わたしたちがはじめに走行体に取り入れた「オンオフ制御」に関して、理論面と実践面の双方から解説しました。

⇒連載バックナンバーはこちら

　今回は、前回のオンオフ制御の欠点を克服するために、オンオフ制御に変わる制御方法の検討を理論面から行いたいと思います。

　オンオフ制御とは、読んで字のごとく「ON（出力あり）」か「OFF（出力なし）」を使い分けて「操作量（出力値）」の“あり”“なし”を決定し、「制御量（入力値）」を目的値に近づける制御です。

　この制御の利点は、とにかく作るのが容易だということです。制御の本質的な部分に限れば、if-else文が1つあれば実装完了です。

　ですが、前回の記事のとおり、オンオフ制御には欠点があります。それはつまり、“オーバーシュート”と“アンダーシュート”を繰り返す「ハンチング」を起こして、制御量が一定にならないという問題です。これは、走行体でいえば、常に左右に旋回を繰り返してしまい、ムダな走行距離が生じてしまうということです。ETロボコンで良い結果を残すためには、タイムロスにつながるようなムダな走行距離の発生を極力抑えることです。そのために、今回は「PID制御」の導入を検討していきます。

　まずは、PID制御とは何か？ というところから説明していきましょう。

PID制御とは

　連載第1回「目指せETロボコン!! ライントレースとシステム制御」の解説のとおり、PID制御自体は古典制御と呼ばれる「閉ループ制御」の一種です。温度制御に使われることが多いので、皆さんの身の回りの家電製品にも使われていることでしょう。

　以下が、そのPID制御の式です。

　いかがでしょうか？ 数学が得意な方はこの式を見ただけでなるほどと思われるかもしれません。しかし、わたしの第一印象はこうでした……。

何これ!? PID怖い!!

　もしかすると、わたしと同じように不安を感じた方もいらっしゃるかもしれませんね。しかし、ご安心ください。今回の内容を読めば、きっとこの数式への不安もなくなるはずです！

　それでは、「教育用レゴ マインドストームNXT（以下、走行体）」へPID制御を導入する効果を理論面から確認しつつ、PID制御とは何か、そしてなぜ怖くないかについて詳しく見ていきましょう。

P、I、Dパラメータのそれぞれの意味と用途

　PID制御では「P」と「I」と「D」のパラメータを用います。

　それぞれのパラメータの意味は以下のとおりです。

• P：比例制御
• I：積分制御
• D：微分制御

　つまり、PID制御とは“比例と積分と微分を使った制御”だということです。

　また、それぞれの制御には、次のような効果があります。

• P制御は、現在の状況に対して操作量を決定する
• I制御は、過去の状況に対して操作量を決定する
• D制御は、未来の状況を予測して操作量を決定する

　これらの制御がどういった働きをするか、1つ1つ確認していきましょう。

P制御導入によるオンオフ制御の欠点の克服

　それでは、オンオフ制御の欠点を克服するにはどうすればいいでしょうか？

　連載第2回「オンオフ制御によるライントレースに挑戦」のパターンAのグラフを見てください。

　オンオフ制御では操作量が一定ですので、オーバーシュートの山の面積やアンダーシュートの谷の面積が操作量の累積に比例し、面積が広いほど走行体はラインに対して急角度で移動することになります。

　偏差が大きいとき――つまり、山の頂上や谷底にいるとき――は、いまにもコースアウトしそうになっている場合ですので、走行体は全力で旋回しつつコースへ復帰しようとします。これは期待どおりの動作です。しかし、その後ラインに近づくにつれ偏差は小さくなりますが、偏差が存在する限り走行体は全力で回転を続けます。そのため、ラインに復帰するときの走行体は、山の頂上や谷底にいるときよりもさらに急角度になってしまい、これがオーバーシュート、アンダーシュートの原因になります。

　ラインに復帰する際は、できるだけ小さな角度で緩やかに戻るのが望ましいので、偏差が小さいときにも全力で旋回する必要はありません。

　そこで、偏差と操作量を比例させる「P制御」を適用しましょう。

　P制御では、偏差×定数で操作量を決定します。偏差が大きければ大きいほど操作量は増大し、小さければ小さいほど操作量は減少します。そして、0付近では操作量もほぼ0になります。P制御を使えば、偏差0付近になったときの角度は、オンオフ制御に比べてずっと浅くなるためオーバーシュートを小さくできます。

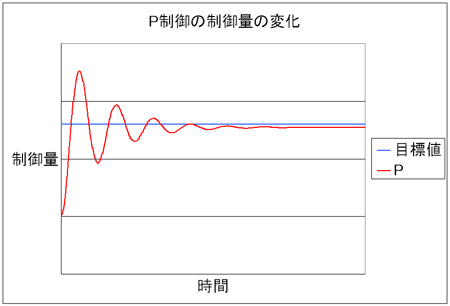
　パラメータ（Kp）が適当であれば、ハンチングは数回で収束し制御量が安定します。

図1　P制御の制御量の変化（1）

　図1は、P制御時の制御量の変化です。オンオフ制御に比べ（前回の記事参照）、ハンチングが数回で収束していることが分かります。

　さて、ここまでが『P制御は現在の状況に対して働く』という説明になります。オンオフ制御では、常に操作量がMAXでしたが、P制御を使うことで現在の制御量に応じた操作量を決定することができます。つまり、“現在の状況に応じて、力の抜き方を決める”のがP制御といえるでしょう。

P制御の2つの欠点

　P制御の導入で、オンオフ制御の問題であるハンチングが発生するという問題は解決しました。

　しかし、P制御には2つの欠点があります。

図2　P制御の制御量の変化（2）

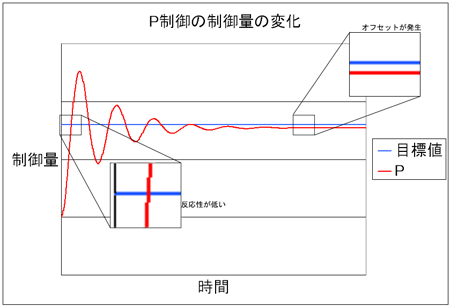
　1つは、偏差が小さいときに操作量が小さくなり過ぎてしまい、制御量が目標値とずれたところで安定してしまうということです。図2のグラフに示したとおり、P制御の制御量は目標値より下側で安定してしまいます。この制御量と目的地の差を「定常偏差」あるいは「オフセット」と呼びます。

　もう1つは、いつも全力のオンオフ制御なら気にしなくてもよかった問題なのですが、制御量が急激に変化した際の反応性が低いという点です。上のグラフで“反応性が低い”と示した場所では、制御量の変化が大きいため、今後目標値から遠ざかることが予想できますが、P制御では現在の制御量のみを操作量の決定に使用するため、操作量は非常に小さな値になっています。そのため、制御量の急激な変化に対応できず、オーバーシュートが発生し反応性が低くなっています。

I制御導入によるオフセットの補正

　さて、オフセットが発生してしまうという1つ目の問題を詳しく見てみましょう。

　ライントレーサの場合、P制御のパラメータ（Kp）が適正であれば、直線を走っているとき制御量は目標値付近で安定します。しかし、カーブがはじまるとオフセットが発生します。

　カーブがはじまったとき、P制御によってその時点ごとの制御量に応じた操作量を決定し、カーブを曲がろうとします。目標値から離れれば離れるほど操作量が上がるP制御ですが、それは長所であると同時に短所にもなります。なぜなら、偏差が小さいと操作量も小さくなり、カーブの最中に偏差0の位置まで戻れず、カーブの外側に寄ってしまうからです。この状態が、目標値と違う場所で安定してしまう“オフセットが発生している状態”です。

　オフセットが発生していてもカーブを抜けられればよいのですが、場合によってはコースアウトしてしまうことがあります。

　では、Kpを大きくし偏差が小さいときの操作量も大きくなるようにしてはどうでしょうか？

　こうすることで、オフセットの発生は防げます。しかし、P制御では現在の値しか見ないため、いま直線にいるのか、カーブにいるのかが分かりません。そのため、P制御でせっかく力の抜き方を決めているのにもかかわらず、P制御のパラメータを大きくすると、カーブの間はいいのですが直線に戻っても操作量が大きくなってしまいます。その結果、せっかくオンオフ制御から改善したハンチングが再発する可能性があります。

　そこで、「I制御」を用いてカーブにいる間だけ、操作量を上げるようにしましょう。

　I制御では、偏差の累積×定数で操作量を決定します。P制御では、現在の状況しか見ないためオフセットが発生していることを検出できず、それに対応することもできません。I制御では、P制御が対応できない小さな偏差も累積させることで、累積値が正負のどちらかにたまるにつれ、オフセットを補正できます。そして、I制御による補正が行われるということは、偏差の累積が十分に大きいということであり、カーブの真っただ中にいるということになります。

図3　P制御とPI制御の制御量の比較

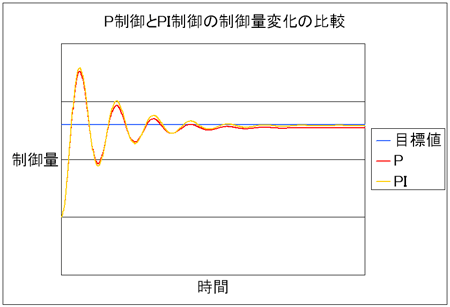
　図3は、P制御時の制御量とPI制御時の制御量の変化の比較です。PI制御時は、オフセットが補正され、目標値近辺で制御量が安定していることが分かります。

　以上、I制御が過去の制御量に対して働く仕組みです。ライントレーサに限れば、I制御は“過去の偏差の累積から現在カーブ中であることを検出して補正する方法”といえるでしょう。