変化のない人生と伝達関数は、あり得ない?:独学! 機械設計者のための自動制御入門(7)(3/4 ページ)
自動制御システムについてのまとめ
自動走行システムを設計する前に、いままでに学習したことを整理しておきましょう。
システムの表現 その1(ブロック線図)
全体システムは、いくつかの小さなサブ・システムから構成されています。
サブ・システムの入出力の関係は、(1)の伝達関数で表現することができます。伝達関数で表現されたサブ・システムをブロックで記述し、それらを線で接続して全体システムの入出力の関係を示したものをブロック線図と呼びます。
ブロック線図で、直列する複数のサブ・システムは伝達関数の乗算によって、1つにまとめることができます。並列する複数のサブ・システムは伝達関数の和算によって、表現することができます。制御系は、制御対象となる伝達関数Gsと、制御対象を制御するための制御器の伝達関数Gcに分離して記述することができます。
フィードバックループを閉じる前の一巡した伝達関数を、開ループ伝達関数(一巡伝達関数と呼ぶ本もある)といいます。
システムの特性:周波数依存性(周波数応答特性)
入出力信号や物理状態は、無数の周波数成分から構成されています。従って、システムの入出力関係も周波数ωに依存します。つまり伝達関数は周波数ωの関数です。 システムの入出力の周波数依存性を示したものが周波数応答特性です。これは、すなわち伝達関数の周波数応答特性を意味しています。周波数応答特性は、正弦波を入力したときの、入出力の振幅比と位相遅れによって表現されます。
システムの表現 その2(伝達関数のラプラス変換と複素数表示)
伝達関数は、システムの入出力についての微分方程式をラプラス変換して、ラプラス演算子sによって記述できます。また、伝達関数は、ラプラス演算子s=iωとおいて、複素数でも記述することができます。これにより、システムの入出力についての微分方程式をたてることができれば、周波数応答特性を計算で求めることができます。横軸を周波数ωの対数表示、縦軸を入出力の振幅比の対数表示および位相遅れを表示したものをボード線図と呼びます。直列する複数のサブ・システムは、各伝達関数の積によって1つの伝達関数に表現できます。積算された周波数応答は、個々の伝達関数の周波数応答の和として求めることができます。
フィードバックシステムの安定性
開ループ伝達関数がGoであるシステムのループを閉じて、フィードバックシステムを構成すると、閉じた後の伝達関数は
となるから、開ループ伝達関数が、
Go(ω)=−1=cos(−π)+i・sin(−π)=cos(-180°)+i・sin(-180°) (18)
となる周波数が存在するとき、フィードバックシステムは発振します。
従って、位相遅れが180°のときの入出力振幅比(伝達関数の絶対値)が1より小さければ小さいほど(ゲイン余裕)、あるいは、振幅比1のときの位相遅れが180°より小さければ小さいほど(位相余裕)、システムは安定となります。
システムの静特性
制御対象Gsの前に外乱δが存在する場合には、フィードバックループを閉じたときの入力xに対する出力yは、制御器の伝達関数をGcとして、(5)式で表されます。
システムの静特性とは、入力値が0から一定値xに変化したとき、あるいは外乱δが作用したときのt⇒∞の応答です。このとき周波数応答ではω⇒0に対応するから、ω⇒0のとき制御器の伝達関数Gcの入出力振幅比またはゲインが∞であれば、外乱δの影響を受けずに、出力yを目標値xに一致させることができます。
以上のことを確認したうえで、いよいよ強風が吹いても目標位置から外れない自動走行システムの設計に取り掛かりましょう。
強風が吹いても目標位置から外れない自動走行システムの設計
まず、何が問題だったか思い出してみよう
図3のように、道路のセンターラインに沿って自動的に運転するよう制御された車が、強風が吹くと、目標値であるセンターラインからずれてしまう。このようなシステムに対して、横風が吹いても、車が目標位置であるセンターラインの上を曲がらずに走るにはどうしたらよいか?っていう話だった
具体的には、タイヤの操舵角1°分に相当する横ずれが発生してしまうほどの強風が吹いているときに、図4のコントローラの設計はどうしたらよいか? っちゅうことだったな
問題のシステムは、目標位置であるセンターラインと車の位置の差である偏差に比例した角度だけハンドルを回して車体の位置を制御しよう、という比例制御やった。図5のステアリングシステムG2は、ハンドルを1°回転させるとタイヤも1°回転する
図6に、ステアリングG2と車体Gsの周波数特性を示している。これらの情報から、強風が吹いてもセンターライン上を走ることができるシステムを設計してごらん
まず(5)と同様に、車の位置Y3は(20)
開ループシステムの伝達関数Go=G1・G2・Gsは、複素指数の公式を利用して
だから、ゲイン、位相はそれぞれ次のようになる。
ゲイン:20・log(|Go|)=20・log(|Go|)=20・log(A1・A2・As)
=20・log(A1)+20・log(A2)+20・log(As) (23)
位相遅れ:∠(G1・G2・Gs)=θ1+θ2+θs (24)
例えば、コントローラG1の設定をA1=2(°/m)とすると、G1のゲインは20・log(2)=6(dB)、位相遅れはθ1=0°だよね。A2、θ2、As、θsについてはさっき叔父さんが示した図6のとおりだよ。従って、開ループ伝達関数Goの周波数応答は図7のようになる
複素数の指数関数を利用すると、ボード線図の素晴らしさがよく分かるな。草太、ほんまに成長したなぁ。叔父さんはうれしいで……
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現



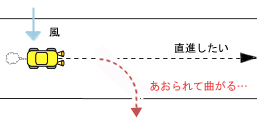 図3 強い横風を受けて曲がる車
図3 強い横風を受けて曲がる車 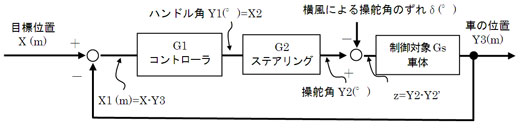 図4 横風を受けるときの自動走行制御システムの構成
図4 横風を受けるときの自動走行制御システムの構成 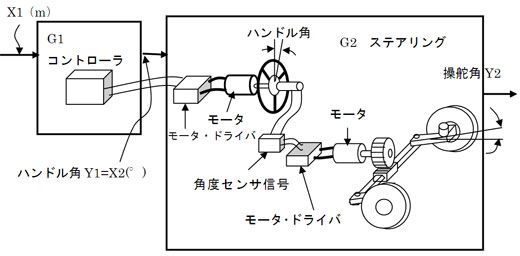 図5 制御器(コントローラG1及びステアリングG2)の構成
図5 制御器(コントローラG1及びステアリングG2)の構成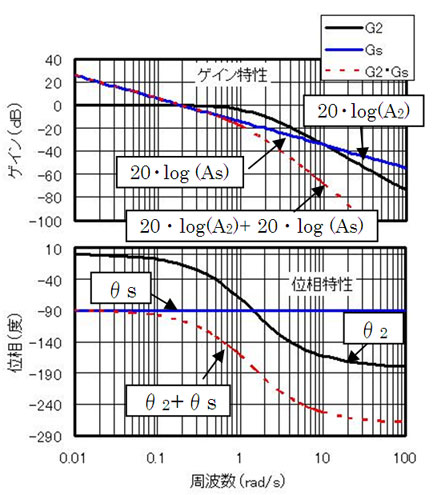 図6 ステアリングG2と車体Gsのボード線図
図6 ステアリングG2と車体Gsのボード線図 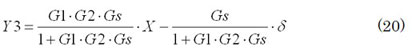
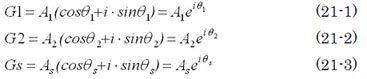
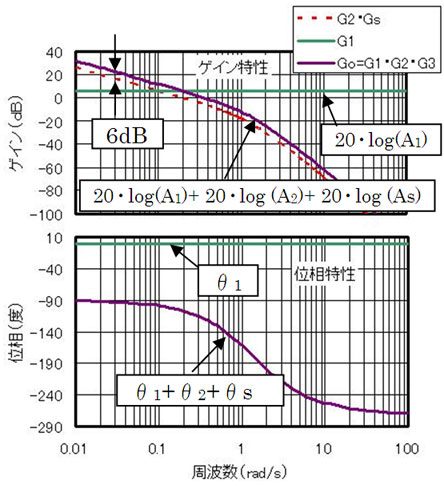 図7 コントロールステアリングG1と開ループGoのボード線図
図7 コントロールステアリングG1と開ループGoのボード線図






