摩擦係数というより摩擦係数の変数だ:ピタゴラスイッチの計算書を作ろう(2)(4/4 ページ)
問題1の解答
2つあります。
解答1
図2.9の草太が設計したスロープの最大傾斜は54度であり、tan(54.5度)=1.4である。
(2-16)式より、最大静止摩擦係数が0.4以上あれば、原則、ボールはスロープ上を滑らず回転しながら移動する。従って、損失エネルギーは転がり摩擦によるエネルギー損失Elossのみが発生する。
転がり摩擦によるボールの単位質量当たりのエネルギー損失は、転がり摩擦係数をμrotと書く。
(1-21)式より以下のようになる。
これはまた、位置エネルギーに換算して表示すると、
と書ける。
図1.6と積分の定義から、
だから、転がり摩擦によるエネルギー損失は位置エネルギー換算により、以下となる。
0.05×350mm=17.5mm
解答2
ボールの回転運動の運動方程式は摩擦力をFとして、(2-1)式となる。
同じく、ボールの並進運動の運動方程式は(2-2)式となる。
(2-1)にω、(2-2)にvを乗じて加えると、
ボールの回転角度をφ、並進移動距離をsとすると
であるから
である。
出発点Aから終点Bまで積分すれば、
となる。
右辺第4項は摩擦によるエネルギー損失であるが、解答1からボールはスロープ上を滑らないからds=rdφであり、よって右理論上は右辺第4項の摩擦エネルギー損失は0である。
しかし実際にはミクロの変形によるエネルギー損失が存在し、その値は転がり摩擦係数μrotを使って以下のように計算できる。
ただし、斜面法線力Nには遠心力は作用しないものとしている。
mgで割って位置エネルギーに換算すると、損失エネルギーは以下のようになる。
以下は解答1と同じため省略とする。
問題2の解答
(2-13)から最大静止摩擦係数が0.3の場合、
tanθ ≦ 3.5μmax=3.5X0.3=1.05
上記を満足する範囲ではボールは滑らずに回転して移動する。その範囲の水平距離をLrotとすれば、解答1の結果から、転がり摩擦による損失は
である。
逆に、残りのスロープの勾配tanθが1.05を超える領域では、ボールは滑りながら移動するから、滑り摩擦によるエネルギー損失は最大静止摩擦係数をμmaxとして、位置エネルギー換算で、
である。
表1のスロープ形状からこう配(tanθ)を計算すると、表2の薄い水色で着色した範囲で勾配が1.05より小さく転がり摩擦が発生していて、その全長は210mmである。
従って、以下のようになる。
- 転がり摩擦によるエネルギー損失は0.05×200=10
- 滑り摩擦によるエネルギー損失は0.3×(350-200) =45
上記を合計すると、55mmとなる。
上記計算において、表2の転がり摩擦から滑り摩擦に変わる部分、またはその逆の部分の位置は、その中間点であると計算している。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
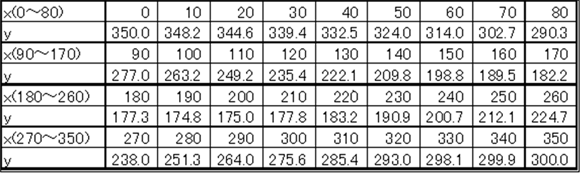
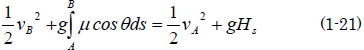
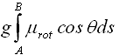
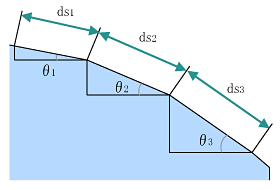 図1.6(第1回より) 曲線を直線に分解
図1.6(第1回より) 曲線を直線に分解 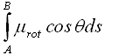
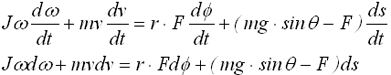
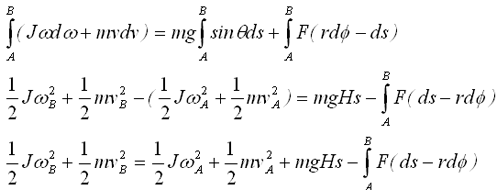
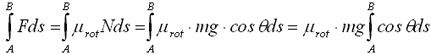
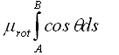
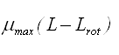
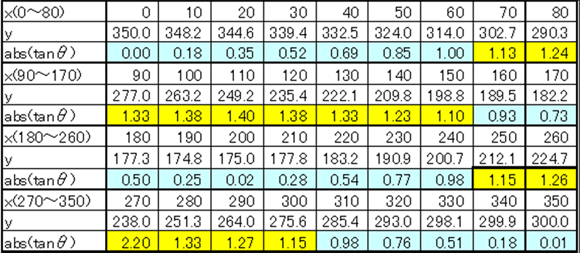 表2 図2.9のスロープの傾斜データ
表2 図2.9のスロープの傾斜データ





