猫とピンポン球と周波数応答特性:独学! 機械設計者のための自動制御入門(2)(2/3 ページ)
周波数応答特性
「周波数応答特性」というのは、自動制御の本には必ず出てくる基本事項です。制御系を構成する要素の周波数応答特性から、その要素がどの程度の「反応の遅れ」と「変化に対する過剰反応」の特性を有するかが分かります。つまり制御系の構成要素の周波数応答特性は、「反応の遅れ」と「変化に対する過剰反応」の定量的な表現であるということができます。以下では、周波数応答特性について学習していきましょう。
周波数応答特性というのは学校で学んだから知っているだろうと思うけど、念のため復習しとこうか。まず、特性を知りたい制御系の構成要素、例えば図1のシステムでいえば、制御部、操作部や制御対象のことやな。この構成要素に、図3のようにある周波数で変化する正弦波の目標値を入力として与える
この周波数を低い値から大きな値に徐々に変化させたとき、その構成要素の出力が目標値に追い付けるかどうかを観察するんや。具体的には入出力の振幅比Y/Xと位相の差θだ。これを周波数ごとにグラフ化したものがその構成要素の周波数応答特性ということや
テレビで、卓球台の前で猫がピンポンを目で追いかけているビデオをよく見掛けるよね。ピンポン球がゆっくり行き来しているときは、猫もピンポン球を追いかけることができるけど、速くなると、追い付けなくなる
いまの猫のビデオを図で説明すると図4のようになる。この場合、猫が構成要素だ。ピンポン球の動きが目標入力、猫の目の動きが出力となる。ビデオや図4から、入力が低周波の場合には猫の目の動きはピンポン球に確実に追い付いているのが分かるやろ
入力の周波数が高くなる、つまりピンポン球の動きが速くなると、猫の目の動きの振幅は小さくなるね。これは、ピンポン球の動きに付いていけなくなったということだね
そうだ。入力の周波数が高くなると出力振幅が小さくなるだけでなく、出力の位相にも遅れが出ている。図5は図4の時間軸の一部を拡大したものだけど、これを見るとそのことがよく分かる
位相ねぇ。この位相という言葉、なんか分かりづらいんだよね
位相が分かりづらければ、時間遅れが発生しているって思えばいい
確かに、ピンポン球が中央から端に行って、また中央に戻りはじめているのに、猫の目の方はあたかもピンポン球がまだ端の方に向って動いているように、追いかけているね。つまり時間遅れがあるってことだね
おぉ、そうか! この時間遅れの大きさが『反応の遅れ』を定量的に表現しているってことか!
そうや! よく気が付いた
ということは『変化に対する過剰反応』は、目の動きの振幅ってこと? でも、過剰反応しているとは思えんけどねぇ
ビデオからも分かるように、ピンポン球を追いかける猫の目の動きはそれほど過剰な反応をしていません。過剰反応する例として分かりやすいのは、コップの中の水や、ばねで結んだ鉄球の運動です。
コップに水を入れて揺らすと、ゆっくり揺らす場合にはコップの中の水は跳ねません。コップを揺らす振幅が小さければ非常に速く揺らしても水面にさざ波がたつだけで水はこぼれません。しかし小さい振幅でも、ある周波数で揺らしてやるとコップの中の水面が大きく揺れ、水が外に飛び出ます。つまり過剰反応をしているわけです。
機械設計者ならばこれを「共振現象」と呼ぶことはご存じですね。同様にばねに結んだ鉄球の運動も共振系ですから、固有振動数付近で過剰反応することは理解できると思います。図6は機械力学のどの教科書にも必ず載っている代表的な共振系の周波数応答特性です。
共振系の場合には、図6のように、ある周波数域だけ過剰反応して低周波域や高周波域では過剰反応しないよな。特に高周波域ではほとんど反応しない
猫の目の運動や共振曲線の例から分かるように、「反応の遅れ」や「変化に対する過剰反応」は、入力の周波数の高低によってその大きさが違います。そこで、横軸に周波数、縦軸に入出力間の振幅比と位相遅れをとって、各周波数におけるそれぞれの特性をグラフにしたものにより周波数応答特性を表すことにしています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

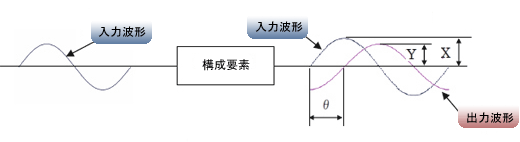 図3 周波数応答
図3 周波数応答 
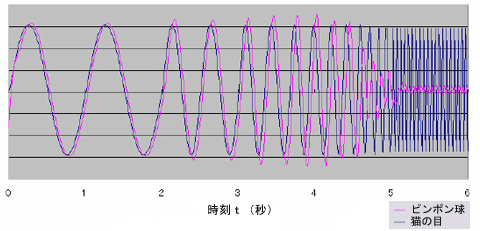 図3 周波数応答 図4 猫の目の周波数応答
図3 周波数応答 図4 猫の目の周波数応答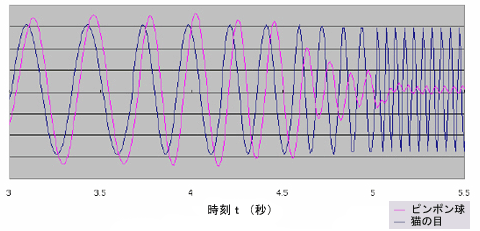 図5 猫の目の周波数応答(図5を拡大)
図5 猫の目の周波数応答(図5を拡大)

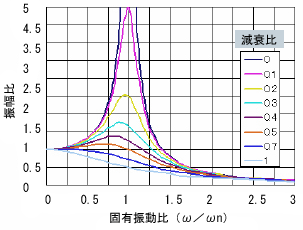 図6 共振曲線の例
図6 共振曲線の例 





