Magnaのスポット溶接点削減大作戦:メカ設計 イベントレポート(7)(2/3 ページ)
基本考察
図4に示す、2つのハット断面(つば付き帽のような形状)のフランジ部をスポット溶接で接合した梁(はり)モデルを用いて、スポット溶接の最適化の基本検証を行った。
フランジ部の左右両側にスポット溶接を設定している。左の丸囲い部が拘束されている領域で、右側の端部に荷重を加えるという単純な片持ち梁(かたもちばり)としている。
ここではスポット溶接の密度に対する感度をチェックした。以下の図5のグラフの脇に並べられた図は梁を上面から見たものである。小さな四角はスポット溶接点である。基準デザインを基にしてスポット溶接の密度を変えた場合、負荷点の剛性がどのように変化するかを可視化したものが図5のグラフである。
縦軸は基準デザインを1としたときの相対剛性、横軸はスポット溶接点の密度である。
まずスポット溶接点の密度を2倍にした場合が、図5の右上の図である。そこから2分の1、4分の1、5分の1……と、スポット溶接点数を減らしていくと、負荷点剛性がどのように変化するのか見ていく。スポット溶接点数が隅に4点のものは、剛性の低下が著しいが、スポット溶接の点数が8点に減るまでの剛性の感度は低くなっている。
次に、スポット溶接点数は基準デザインと同じだが、配置パターンを変えてみたもので検証した。図6の右上の図では、打点を極端に左へ寄せている。配置の仕方が悪いと、先ほどの結果のスポット溶接点数が4点の場合とほぼ同等の剛性しか得られないということが分かる。つまり、打点数だけではなく配置パターンによっても剛性が変化するということが分かった。
スポット溶接点の配置を検討するにあたって、先述したハット断面の梁モデルを用い、剛性の最適化を検証した。スポット溶接はRBE3とソリッド要素によるモデルを適用した。
疲労寿命予測ソフト(FEMFAT)が対応するスポット溶接の解析モデルは、現在、次の4つ(図7)。
スポット溶接点の配置が自由に調整できるよう、あらかじめスポット溶接点の密度を2倍にしておく(図8)。
(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
剛性の最適化では、「スポット溶接点数は基準デザインと同じである」「たわみ量を最小にする」ということを条件とした(ここではトポロジー最適化のプロセスの中で、ソリッド要素のヤング率を無効化した)。
図9は負荷点変位の比較をしたグラフである。
基準デザインの負荷点変位に対して、最適化後の負荷点変位がどうなったのかというグラフを見ると、最適化後の負荷点変位が1.6%減少している。つまりスポット溶接点数は同じなのに負荷点変位が減少したという結果が得られた。また1.6%減少した負荷点変位は、スポット溶接点数が2倍のときとほぼ同等だということが分かった。スポット溶接点の接合パターンが変化することで、剛性が大きく変化するということが確認できた。
以上の結果により、スポット溶接点数が同じであっても、配置によっても剛性を最適化できるということも確認ができたという。
疲労解析の最適化について説明する。先述の検証と同様に、スポット溶接点数は変えずに、疲労損傷度を均一化するという条件で計算した。その結果を示したのが図10である。
(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
剛性最適化の結果と似ているが、中央部のスポット溶接接合パターンが微妙に異なる。また、耐久性能を最適化することで、剛性が基準デザインよりも1.6%上昇した。繰り返し計算回数は46回だった。
耐久性能結果の比較
図11は耐久性能結果のプロット、スポット溶接点における疲労損傷度の結果を可視化したものだ。
(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
グラフの左側が拘束点側、右側が負荷点側となっている。グラフの印は、スポット溶接点での疲労損傷度となる。基準デザインのデータは茶色線で、やや左上がりで拘束点の疲労損傷度が一番高く、次に負荷点が高くなっている。最大値と最小値の開きも大きい。疲労最適化をしたものは黄色線で、最大値と最小値の開きが小さくなっていることが分かる。
次に疲労最適化に関して、スポット溶接のモデルをRBE3/ソリッド要素からビーム要素に変え、先述と同様の比較を行った(図12)。
(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
モデルを変更しても、最適化が可能であることが分かった。また、前ページで説明したの4種類の対応モデルすべてについて適用が可能だということも確認したという。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
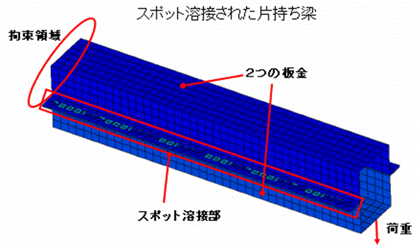 図4 基本検証に用いた梁モデル(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
図4 基本検証に用いた梁モデル(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)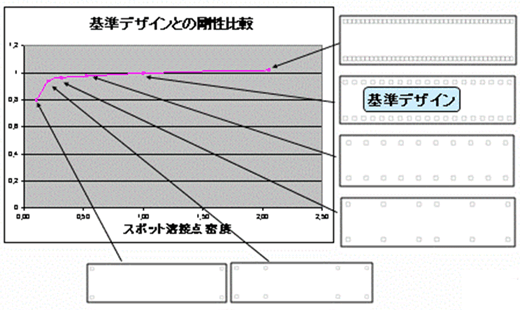 図5 スポット溶接の密度に対する剛性の感度(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
図5 スポット溶接の密度に対する剛性の感度(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)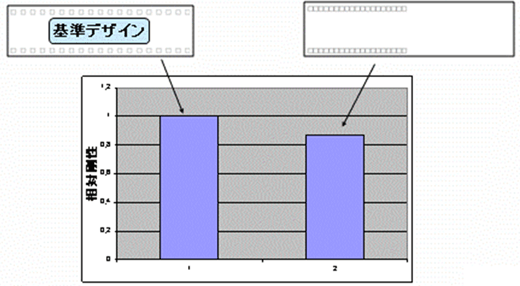 図6 スポット溶接点の配置パターンによる剛性への影響確認(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
図6 スポット溶接点の配置パターンによる剛性への影響確認(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)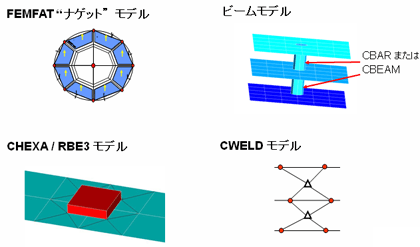 図7 スポット溶接のモデル化(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
図7 スポット溶接のモデル化(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)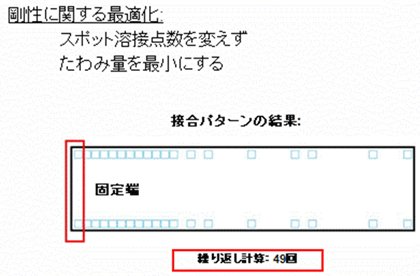 図8 梁モデルによるスポット溶接点の最適化検証(剛性の最適化:接合パターン)
図8 梁モデルによるスポット溶接点の最適化検証(剛性の最適化:接合パターン)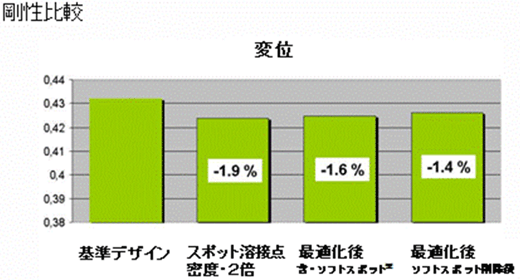 図9 梁モデルによるスポット溶接点の最適化検証(剛性の最適化:グラフ)(マグナ・インターナショナル・ジャパン プレゼンテーション資料より)
図9 梁モデルによるスポット溶接点の最適化検証(剛性の最適化:グラフ)(マグナ・インターナショナル・ジャパン プレゼンテーション資料より) 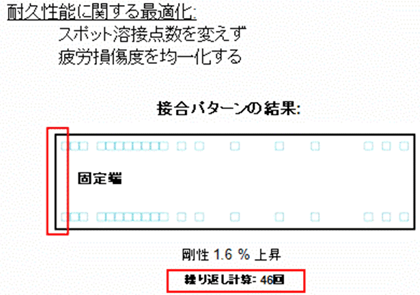 図10 梁モデルによるスポット溶接点の最適化検証(耐久の最適化:接合パターン)
図10 梁モデルによるスポット溶接点の最適化検証(耐久の最適化:接合パターン)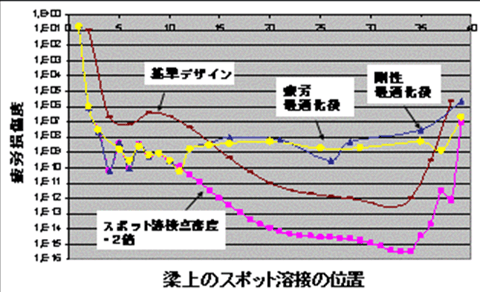 図11 梁モデルによるスポット溶接点の最適化検証(耐久の最適化:グラフ)
図11 梁モデルによるスポット溶接点の最適化検証(耐久の最適化:グラフ)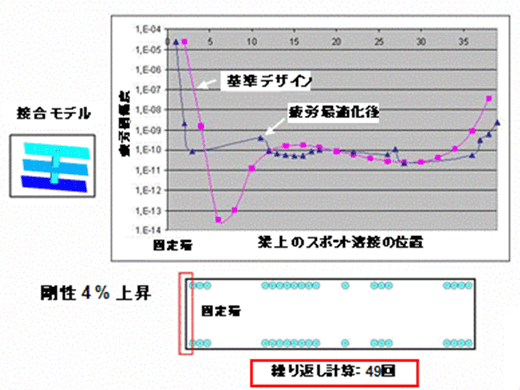 図12 梁モデルによるスポット溶接点の最適化検証(耐久の最適化:ビーム要素モデル)
図12 梁モデルによるスポット溶接点の最適化検証(耐久の最適化:ビーム要素モデル)





