幾何公差? とにかく指示しときゃーいいでしょ:演習系山田式 機械製図のウソ・ホント(6)(1/2 ページ)
幾何公差の表記作法、あなたはしっかり理解している? いいかげんに幾何公差を指示するとトラブルのもとになるので要注意だ。
前回出題した【問題5】の解答を以下で解説していきます。幾何公差のイメージは理解していても、表記作法を厳密に理解していない技術者はたくさんいると思います。いいかげんに幾何公差を指示してしまうと解釈が異なりトラブルのもとになりますよ。本課題を通して、JIS製図における幾何公差の作法を習得してください。
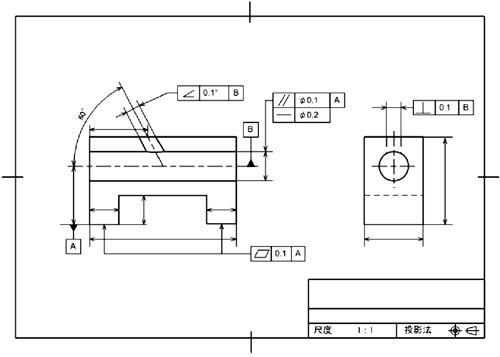
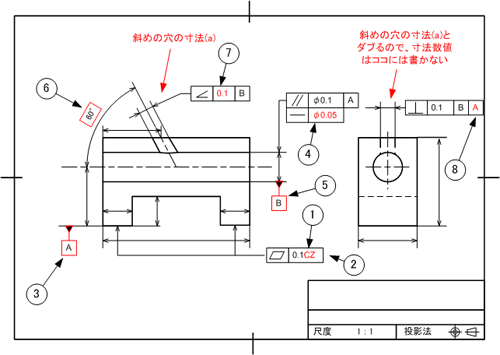
【問題5】の解答
ポイント1
同一面上の離れた形体に平面度指示する場合、出題された平面度の表し方では、左右それぞれの面が独立して平面度0.1mm以内にあればよいという意味になります。ここでは取り付け面であると思われるため、左右共通に0.1mm以内にある方がベターですので、共通領域を表す「CZ」を幾何公差値に続けて記入します。
ポイント2
平面度は形状公差ですから、データムは必要としません。平面度とは「その面を絶対値、つまりその面が寸分も狂いがない“真っ平ら”だと考えると、そこからどれだけずれても(あるいはゆがんでも)よいか?」を規制するものです。
ポイント3
本課題で示した下面を「データムA」として設定するのですが、寸法線の延長線上にデータムを付与すると、その寸法の中心線(または中心平面)をデータム面と定義してしまいます。ここでは明らかに下面を指示しなければいけないため、寸法線から明らかに離した位置にデータムを指示しなければいけません。
ポイント4
複数の幾何公差が相互関係にあるとき、「位置公差>姿勢公差>形状公差」の関係が成り立ちます。本課題では、姿勢公差である平行度の公差値より形状公差である真直度の方に厳しい数値を与えなければいけません。
ポイント5
旧JISでは中心軸線上にデータムを指示することができましたが、現在のJISでは中心軸にデータムを直接指示することができません。軸線をデータムとする場合は、寸法線の延長線上にデータムを指示しましょう。
ポイント6
傾斜度の角度寸法は理論寸法として表さなければいけません。理論寸法を表すため角度寸法を四角い枠で囲みます。
ポイント7
傾斜度公差にかかわらず、幾何公差値は範囲を表します。従って角度で幾何公差を指示できないため、理論的に正しい角度からのずれ幅を規制しなければいけません。ここでは、理論的に正しい60度の線を中心にして±0.05mmの領域に斜面が入っていればよいことになります。
ポイント8
正面図で斜めに開いた穴でも右側面図から見て直角であってほしい場合、データムBだけを基準にすれば、360度の中でどの方向に開いていてもデータムBに対して直角であればよいことになります。鉛直方向に直角度が欲しい場合は、鉛直を定義するためデータムAを参照します。今回の解答例では、第1優先をデータムB、第2優先をデータムAとしましたが、設計意図によっては逆になる場合もあります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 奥行き表現やトラッキング機能を強化したVR設計検証支援システム